19世紀ボヘミアのブラシュカ父子が作った、美しく、かつ解剖学的に正確な、海洋生物のガラス模型たち。二人は製造法を秘密にしていて、二人が死んだあとに多くの人が再現を試みたが成功していないそうなhttps://t.co/mV3O1xKoC5
— ultraviolet (@raurublock) May 4, 2019
π^xの振る舞いにどこかで見覚えがあると思ったら「クラゲの泳ぎ方」なんですね。
GWほとんどこれ作るのに費やしてしまったけどとりあえず完成。。
— はのば (@hannover_bloss) May 4, 2019
リアルタイムにグリグリ動かせます。
あとはArtStationにメイキングとか載せておく。 #UE4 pic.twitter.com/O23SsViXid
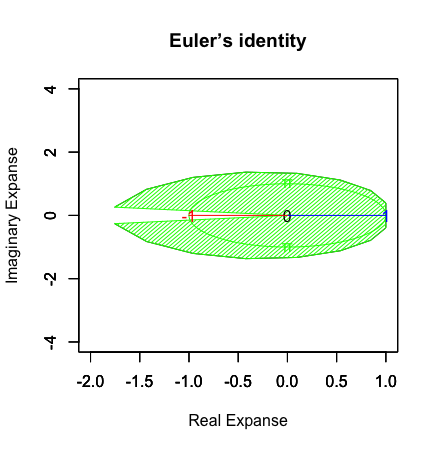
①N(分割数)=1の時、観察対象の広がり(Expanse)、すなわち観測原点「0」からの視界(Perspective)は、とりあえず観測原点「0」から距離「1」先で任意の観測点と接する「半径πの円盤」と映る。これはまさに古代メソポタミア地方(チグリス・ユーフラテス川流域)や、エジプト王朝(ナイル川流域)やフェニキア人交易圏(地中海・黒海沿岸全域)や、ギリシャ人植民圏(ギリシャ半島中心にアナトリア半島やイタリア半島や南仏まで含む)や、古代ローマ帝国(地中海・黒海沿岸に加え中東進出を企てる)や、イスラム文化圏といった地中海沿岸地域を「文明圏」とし、これを「未開人が跋扈する辺境地帯」や「大海の向こう側にある世界の果て(絶えず滝の様に海水が流れ続けており、その向こう側で大海蛇(Giant Sea Serpent)が獲物が落ちてくるのを待ってる)」を同心円状に配置した正距方位図法(azimuthal equidistant projection)めいた古代地図の背後にあった地理感覚そのもの。
②Nが増大するにつれ、それは急速に観測原点「0」を観察対象「1」を中心に覆わんとする半球へと成長を遂げていく。実際には「半球」というより「3/4球」という感じ。そもそも複利計算式(1+1/N)^Nがベースになってるくらいだから、出足の伸びは物凄くグイグイ迫ってくる。かくして大航海時代以降「人類未踏の地」は急速に縮退し、20世紀に入ると南極やチョモランマ山渓、さらには深海や宇宙といった僻地に限定されるまでに至る。
③Nが十分に増大すると、それは観測原点「0」を覆う全球としか映らなくなるが、それでもなお決して極限値「−1」に到達する事はない。かくして「人類の認識可能範囲外を跋扈する絶対他者」は海底で眠る巨大怪獣や流星に付着して地球に到達する流行病、不可視の次元より襲来するフランク・ベルナップ・ロング「ティンダロスの猟犬(The Hounds of Tindalos、1929年)」における使役動物、さらには電波や放射能の類似物といった特殊な形態でしか存在し得なくなる。
そもそも「泳ぐ」とはどういう事か。クロールや平泳ぎなどの経験からすると…
- まず進行方向に向けて体表面や体積を最大値に到達させる。
- 進行方向に向けて(流線型を意識して)体表面や体積を最小限に変形させつつ体を前方に押し出し、後方に送り出せる限りの水を送り出す。
クラゲの泳ぎ方の場合…
- まず「傘を広げ」正面に向けての体表面を最大化させる。
- 次いで「傘を閉じ」ドーム型の前半身を正面に押し出しつつ、後方に送り出せる限りの水を送り出す。
その途中過程で顕現する「体積を最大化させた状態」は微分計算で求める事が出来たりもするのです。
神永 正博「超」入門 微分積分 (ブルーバックス) 「微分は下心をもってせよ」 より
とりあえず「最もアイスクリームを詰め込める理想の円錐」の半径をx(cm)と置く。
- 三平方の定理より「コーンの深さ=sqrt(100(10^2)-x^2)(cm)」が求まる。なお、ここでは話を単純化する為にコーンの厚みは無視して体積と同じとする。底面積はπx^2(cm2)。
- 円錐の体積の公式「底面積(πx^2)*高さ=コーンの深さ(sqrt(100-x^2))*1/3」から「y=1/3*π*x^2*sqrt(100-x^2)」。グラフ化するとおよそ半径8cm辺りに最大値がくる。
#最もアイスクリームを詰め込める理想の円錐
Icecream_corn<-function(x){1/3*pi*x^2*sqrt(100-x^2)}
plot(Icecream_corn,xlim=c(0,10),ylim=c(0,400),type="l",main="The volume of Icecream corn", xlab="x", ylab="y")
こうして問題は「yが最大値となる様なxを求める」という方向に整理される。
- 式中にルートが含まれるのが煩雑。「容積が最大」という事は「容積の2乗も最大」だし、「容積の2乗が最大」なら「容積も最大」なので2乗して「y^2=1/9*pi^2*x^4(100-x^2)」とする。
- このうち1/9*pi^2は定数なのでxが変化しても変わらない。すなわちf(x)=x^4(100-x^2)=100*x^4-x^6におけるxの最大、すなわちf'(x)=0(微分=0、接線の傾きが0)となるxを求めればいい。
Rでの検証例
#微分(Differential)x^4=4x^3
D01_01<-expression(x^4)
D(D01_01,"x")
4 * x^3#微分(Differential)x^6=6x^5
D01_02<-expression(x^6)
D(D01_02,"x")
6 * x^5
すなわちf'(x)=400*x^3-6*x^5=x^3*(400-6*x^2)
x^3*(400-6*x^2)=0 つまり 400-6*x^2=0
つまり 6*x^2=400 つまりx^2=400/6
#x=sqrt(400/6)
sqrt(400/6)
[1] 8.164966
#高さ=コーンの深さはsqrt(100-x^2))=sqrt(100-sqrt(400/6)^2))=sqrt(100/3)
sqrt(100/3)
[1] 5.773503全体的に菅笠の様な形となる。まさしく「傘を開いたクラゲ?」
グラフ化してみる。
#体積が最大化されたアイスクリームコーン
f0<-function(x){sqrt(100-x^2)}
plot(f0, xlim=c(-10,10),ylim=c(0,10),type="l",main="Ice Cream Cone Problem", xlab="x", ylab="y")
polygon(c(0,sqrt(400/6),-sqrt(400/6)), #x
c(0,sqrt(100/3),sqrt(100/3)), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色

無視するしないの境界線
強引に感じた読者も多いと思う。なぜ積分では細部に意味があり、微分では細部を無視しても良いのか。何を無視して何を無視してはいけないか判然としないじゃないか。
この強引さは微積分が「目的」を持っている事からくる。微積分で最も重要なのは目的をかなえられる程度に細部を無視し、近似する事にある。下心を持ちながら、何らかの成果を狙ってやっている事なのだ。
微積分は純粋な興味だけで発展してきた数学ではない。そこに登場する様々な概念や計算技術は理由もなく出てきたものではなく、必ず目的意識が付帯する。体系化された学問とはいえ、実際のところそれは「こう考えたらうまくいった」試行錯誤の結果得られた知恵を編集したものに過ぎないのである。細かい部分が重箱の隅として無視出来るかどうかは「そこからポジティブな成果物が出てくるか」で判断される。要するに成果主義なのである。
まさにこの段差が「想像上の放射相称生物(Imaginaly Radiata)」と「想像上の左右相称生物(Imaginaly Bilateria)」の狭間や「オイラーの等式(e^πi=-1)」と「オイラーの公式(e^Θ=CosΘ+iSinΘ)」の狭間には横たわり「有用と判定された何か」だけが、強引にそれを軽々と飛び越えていくという次第。
Rによる検証例
#半径rの円の面積(pi*r^2)をrで微分(Differential)すると円周の長さ(2*pi*r)となる。
D01<-expression(pi*r^2)
D(D01,"r")
pi * (2 * r)#半径rの球の体積(4/3*pi*r^3)をrで微分(Differential)すると球の表面積(4*pi*r^2)となる。
D02<-expression(4/3*pi*r^3)
D(D02,"r")
4/3 * pi * (3 * r^2)
これぞ「距離1の線分の旋回範囲に、それを半径とする円や球面を形成する」オイラーの原始量(Euler's primitive sweep)の世界…