こうして私の脳内に「基本円(Unit Circle)/基本円柱(Unit Cylnder)/基本球面(Unit sphere)からの脱出口」を見出したティンダロスの猟犬こと正2/(2N+1)角形群が私の記憶を探って新たなビジュアルを手に入れようとしています。例えばエッシャーのだまし絵とか…



最近、水木しげる画伯を追う形で「あちら側の世界」に存在をシフトされた吾妻ひでお画伯が最後に残したこういう絵とか…
その3 pic.twitter.com/2EvCHpsFt8
— 吾妻ひでお (@azuma_hideo) June 6, 2017
あけましておめでとう pic.twitter.com/U7eDlfNrYt
— 吾妻ひでお (@azuma_hideo) January 1, 2017
この先が進めない、どうしたら良いでしょう、やる、やらない? pic.twitter.com/t7Q3Jkhtak
— 吾妻ひでお (@azuma_hideo) February 11, 2019
何とか対策を練らないと、このサイトが「あの手はなんだ、窓に!窓に!」みたいな一文を残して更新を停止する羽目に陥ってしまいそうです…
①とりあえず、これまで扱ってきたオイラーの公式(Euler's formula)cos(θ)+sin(θ)iをより一般化した方程式(Equation)cos(θ)+cos(θ-π/N)iついて。ここでいうNは正多角形(
Regular Polygon, Regular N gon)の角数(NoC=Number of Corners)というより、正多辺形(Regular PolySides, Regular N sides)の辺数(NoC=Number of Sides)と考えた方が都合が良いので方程式の呼称を「正多辺形方程式(Regular PolySides Equation)」に改めます。 既存投稿に莫大な範囲で影響が…
「物理学と数学の狭間」関係?
「円周率の近似」から「基本円/基本円柱/基本球面」まで。
「ピタゴラスの定理」と曲率
「オイラーの公式」から「正多辺形方程式」や「辺長サンプリング効果」まで。
最大の問題点は「学校で生徒に教える」みたいな経験が皆無の為、どうやって纏めたら人に分かり易く伝えられるか見当もつかない辺り…
②ところで、以下の投稿で検討した「どうして正多辺形方程式(Regular Poysides Equation)cos(θ)+cos(θ-π/Nos)iから見放された正方形の世界でオイラーの公式(Euler's formula)cos(θ)+sin(θ)iが成立するのか(辺長サンプリング効果だけでは説明がつかない)問題自体についてはあっけなく突破口が開けました。そう、計算幾何学の世界において正方形は1種類ではなかったのですね。

- 正多辺形方程式(Regular Poysides Equation)cos(θ)+cos(θ-π/Nos)iから見放され、オイラーの公式(Euler's formula)cos(θ)+sin(θ)iも通用しない「呪われし正方形」
統計言語Rによる「呪われし正方形」実現例
c0<-seq(0,2*pi,length=60)
cx0<-cos(c0)
cy0<-sin(c0)
plot(cx0,cy0,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Square in Cos(θ) + Cos(θ-π/4)i",xlab="Real",ylab="Imaginal")par(new=T) #上書き
c1<-seq(0,2*pi,length=5)
cx1<-cos(c1)
cy1<-sin(c1)
plot(cx1,cy1,asp=1,type="l",xlim=c(-1,1), ylim=c(-1,1), main="",xlab="",ylab="")
#塗りつぶし
polygon(cx1, #x
cy1, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
- 正多辺形方程式(Regular Poysides Equation)cos(θ)+cos(θ-π/Nos)iとの関係を断ち切ってオイラーの公式(Euler's formula)cos(θ)+sin(θ)iを通用させる道を選んだ「祝福されし正方形」
統計言語Rによる「最も単純な描円アルゴリズム」実現例
c0<-seq(0,2*pi,length=60)
cx0<-cos(c0)
cy0<-sin(c0)
plot(cx0,cy0,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Square in Cos(θ) + Sin(θ)i",xlab="Real",ylab="Imaginal")par(new=T) #上書き
c1<-seq(0,2*pi,length=5)+pi/4
cx1<-cos(c1)
cy1<-sin(c1)
plot(cx1,cy1,asp=1,type="l",xlim=c(-1,1), ylim=c(-1,1), main="",xlab="",ylab="")polygon(cx1, #x
cy1, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
そう「45度ズレてる」のがオイラーの公式(Euler's formula)cos(θ)+sin(θ)iが通用しない原因だったのですから、さらに45度ズラせばよかったのです。ところで対応する数理は?それとも「昔の数学者は、そんな細かい事は気にしなかった」がファイナルアンサー?
- まぁ、複素平面が未発見で「マクローリン級数による近似が円を描かない」点がスルーされた結果、その事がオイラーの公式(Euler's formula)cos(θ)+sin(θ)iの広まる支障になる事がなかった先例もあるので、悪いことばかりとも言えない?
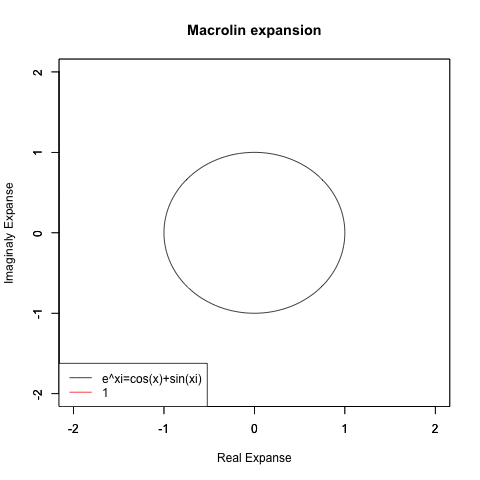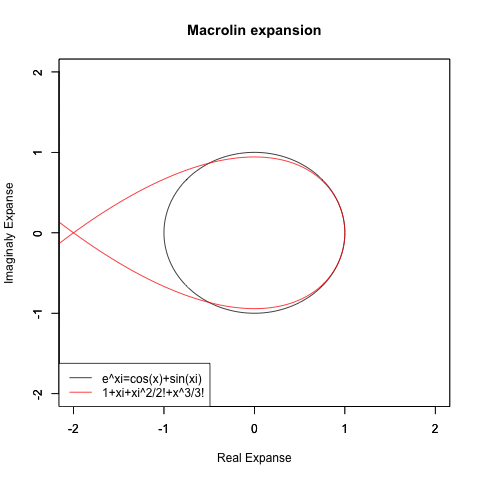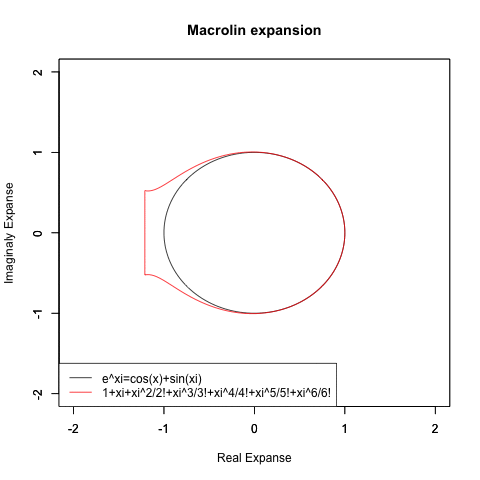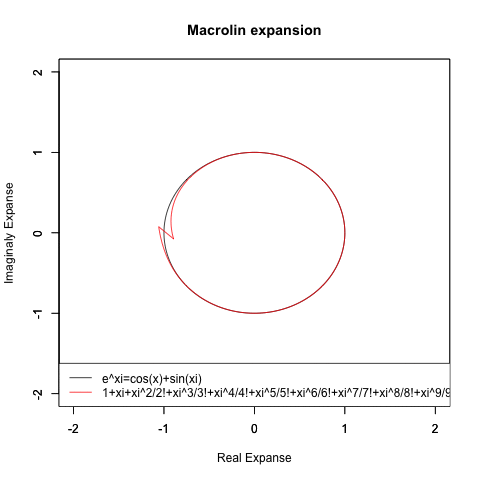
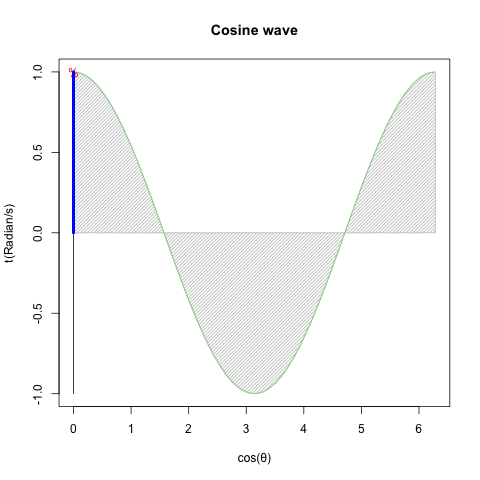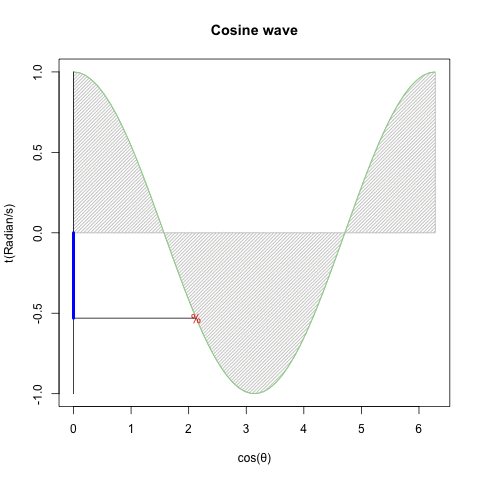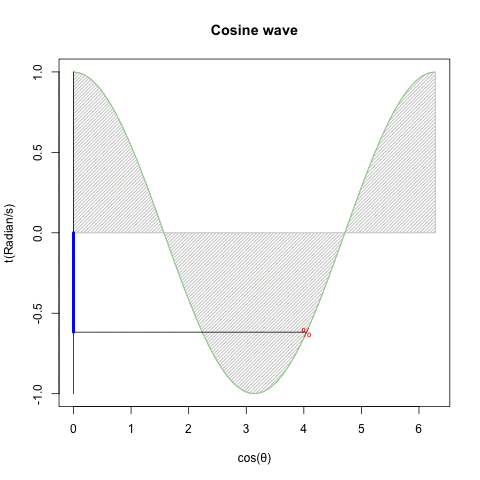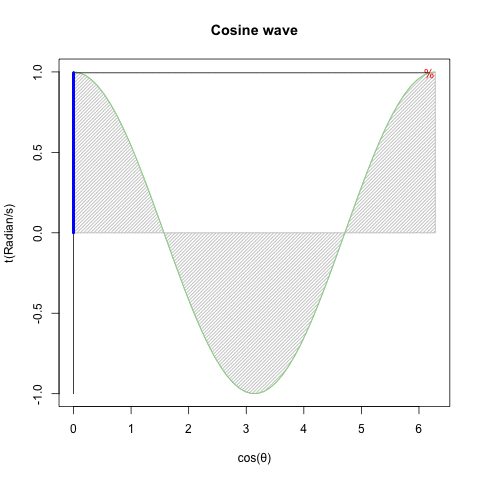
- さらに豪腕なのが「細けぇ事はいいんだ。要するにCos(θ)波とSin(θ)波を直交させれば円を描く、それだけ分かってれば何の問題もないだろうが!?」と主張する物理学勢とも。ただし、この考え方にはプログラマー勢も大半が同意?
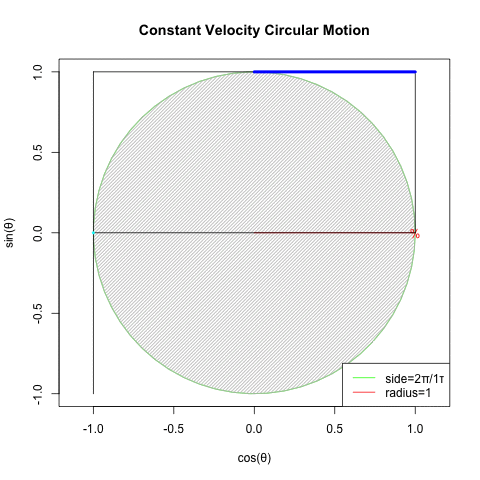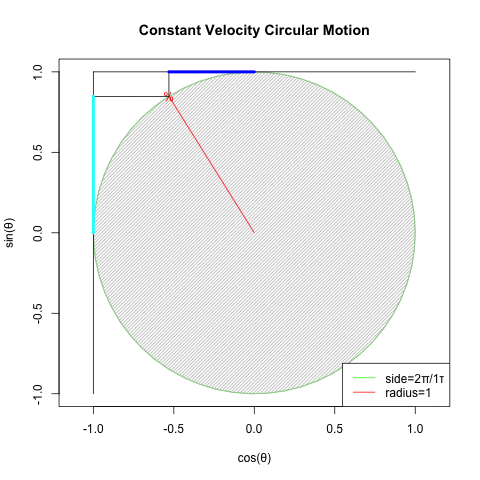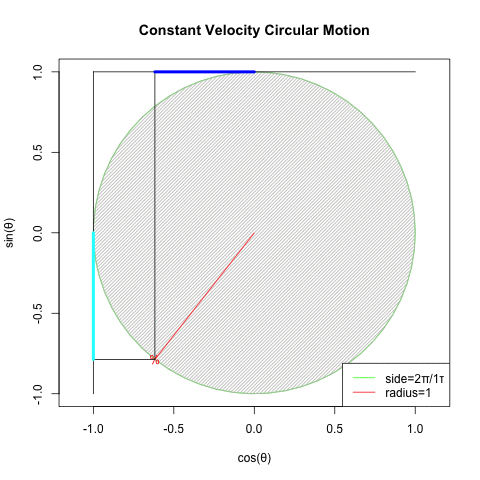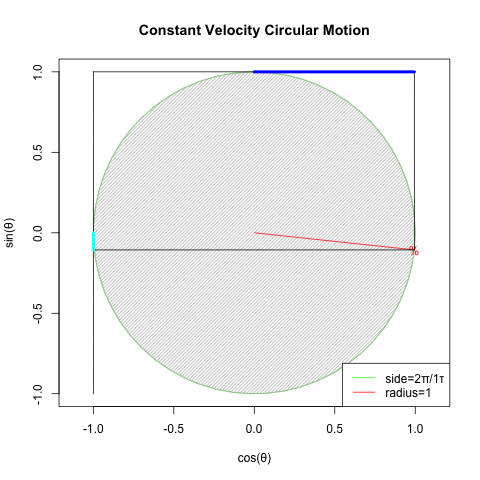

ところで「ティンダロスの猟犬(The Hounds of Tindalos)」には「真円に封印される」という襲撃される側には有り難い事この上ない属性が存在する訳ですが、実はこの概念を正2/(2N+1)辺形群(Regular 2/(2N+1)sides group)に投射すると「真円こそ正2/(2N+1)辺形群の筆頭たる正2辺形(Regular Bilateral)そのもの」という、新たな問題に突き当たる展開を迎えるのです。

- 「観測原点が球上の1点である事しか分からない」1角形が「観測原点1が、如何なる観測結果も円周の半分のπとなる対蹠点-1を発見し正二角形(Regular bilateral)に昇格する確率は?」ベルヌーイ及びその弟子オイラーは式(formula)(1-1/N)^Nから1/e=0.3678794を導出。
統計言語Rによる確認例
#オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1-1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="Natural logarithm", xlab="N", ylab="(1-1/N)^N")
#自然対数1/eと比較。
abline(h=exp(-1))#exp(-1)=0.3678794...
- 円周上にしか存在し得ない正二角形(Regular bilateral)の2辺の長さは、観測値1の場合には直径2と同一視せざるを得ないが、観測値の増大につれ次第に球面上にしか存在し得ない図形的特徴を反映してπ(3.141593)へと近づいていく。この過程を複式簿記による利益計算に擬えると増加率はどうなるか? ベルヌーイ及びその弟子オイラーはこの考え方から式(formula)(1+1/N)^Nよりe=2.718282を導出。
統計言語Rによる確認例
#ヤコブ・ベルヌイの複利計算法に基づく算出方法
f0=function(x){(1+1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(1,3),lty =1,main="Natural logarithm", xlab="N", ylab="(1+1/N)^N")
#自然対数eと比較。
abline(h=exp(1))#exp(1)=2.718282...
- こうやって自然指数関数(Natural Exponential Function)e^xと自然対数(Natural Logarithm Function)log(x)の概念を固めたベルヌーイの弟子オイラーが(当時英国中心に研究されていた)マクローリン級数の援用を受けて完成させたのがオイラーの公式(Euler's formula)cos(θ)+sin(θ)iとなる。

ひゃあ、とどのつまり…
- これまでティンダロスの猟犬(The Hounds of Tindalos)正2/(2N+1)辺形群の封印手段として周知されてきた「真球」そのものがティンダロスの猟犬(The Hounds of Tindalos)正2/(2N+1)辺形群の筆頭たる正2辺形(Regular Bilateral)だった。要するに彼らを封じ込めておけるのは彼らの眷属のみという「法螺吹き上等!?」の創作界も吃驚も展開…
- おそらくこれ以降の言及では「ティンダロスの番犬(The Watchdog of Tindalos=正2辺形(Regular Bilateral))」と「ティンダロスの保護観察対象犬(The Probation target dog of Tindalos=それ未満の正2/(2N+1)辺形群)」を呼び分ける必要が生じてくる。
まだ今すぐにはまとめ切れないけど、何だか新展開の予感?
