
【久遠(くおん,きゅうえん)】 の解説
1 仏語。長く久しいこと。遠い過去または未来。
2 ある事柄がいつまでも続くこと。永遠。「久遠の理想」
過去投稿だとこれの中で宮沢賢治やキェルケゴールやエンルスト・ユンガー辺りを引き合いに出して触れてる概念ですね。
- 今読み返すとキェルケゴールには触れてないっぽい。補足しておくと宮沢賢治が傾倒した法華経の「久遠の仏」概念とキェルケゴールの「誰しもが心の奥底に宿しているイエス・キリスト」概念は親近性が極めて高いのである。
- また(観察者は観測によって得られる確率論的観測結果と通じてしかこの現世そのものに迫れないと考える)確率密度空間(Probability Density Space)の概念を導入すると、(唯識論の出発点となった)龍樹「中論」で理想視される「三昧の境地=観測者自身の定めた精度基準をクリアした観測結果に基づく、観測者自身の思惟のみで構成される世界」が科学的実証主義(Scientific Positivism)の目指すべき立場と重なる。これがまた法華経の「久遠常在」概念やエンルスト・ユンガーの「魔術的リアリズム(Magic Realism)」概念と重なってくる訳である。その事と表裏一体を為すのが近代戦を席巻した「総動員」概念とも。
かかる「唯識三昧の世界」の代表例の一つたる「数理(Mathematical Things)の世界」は「(周到な吟味によって厳選された観察結果のみに立脚する)科学三昧の世界」に「現世そのもの=何もかも複雑に結びついて切り分けて考えられない混沌とした縁起の世界」の混乱が持ち込まれない様にある種の絶地天通を敢行しました。すなわち「加法単位元(Additive Identity)=無限遠点(Inf(inity))-無限遠点(Inf(inity))=0」「乗法単位元(Multiplicative Identity)=無限遠点(Inf(inity))/無限遠点(Inf(inity))=1」といった超越演算(Transcendental Operation)を経てそもそも計測不可能な諸概念を無限大(Inf)や無限小(-Inf:=0)の向こう側に押しやる様になったのです。
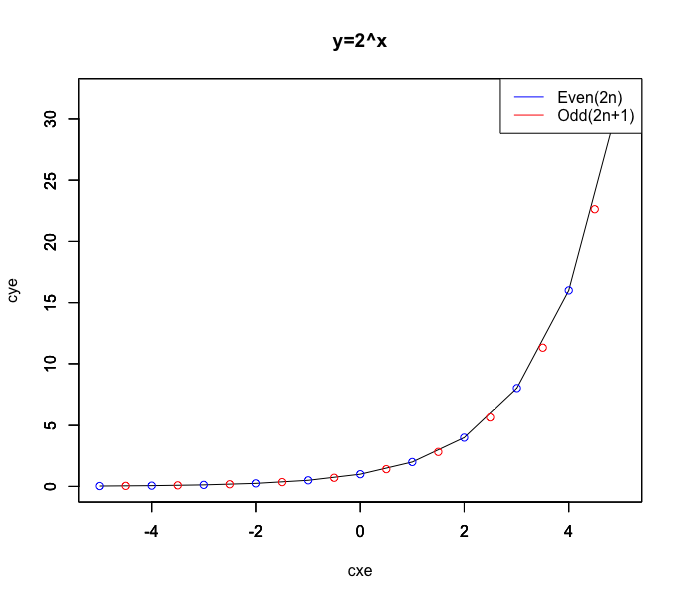
こう主張すると一見宗教的に深まった様に見えますが、実際には深淵に至る思索なんて片っ端から無限遠の彼方(Event Horizon)に追いやられてしまい「偶奇性(Evenness)の起源」みたいな基本的数理からの再出発を余儀なくされる次第。畜生、こいつらですら全然RPG序盤に登場する雑魚モンスターなんかじゃないぞ!!
何せ「分身の術」まで駆使しやがるのです、こいつら…

かくして数理の世界は自明の場合(Trival Case)として自衛武器として「無限大(Inf)や無限小(-Inf:=0)と計測可能空間を峻別する道具」を大量に備える様になった訳ですが、その代表例の一つがユークリッド計量(Euclidean Metric)sqrt(x^2+y^2+z^2…)を一般化したLp空間となる様です。
上図は各p-ノルム(p-Norm)の単位円(Unit Circle)における第一象限、すなわちXY座標{1,0}-{0,1}間の経路を表しています。現時点では理屈は不明ながら途中でXY座標{0,0}を経由するのがL0ノルム、XY座標{1,1}を経由するのがL∞ノルムと規定され(前者を有向グラフx→y,後者を有向グラフy→xの推移と置く説明もある)、Lp空間そのものは両者を含まない、すなわち無限小(−Inf(inity):=0)<p<無限大(Inf(inity))の範囲で展開。ユークリッド計量はL2空間すなわちp=2,中心はL1空間すなわちp=1。
- そういえば、このサイトの中心課題の一つたるオイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)もY軸にCos(θ)を配し、X軸の極少(Nos=-Inf:=0)を-Cos(θ)、極大(Nos=Inf)をCos(θ)と規定した上で両者を含まない形、すなわち0<Nos<Infの範囲で展開する。この場合は中心(Nos=2)がSin(θ)となり、ちょうどオイラーの公式Cos(θ)+Sin(θ)iの成立条件を満たすのである。

あ、そうか。どうしてこれまでこんな簡単な基本的事実に気付かなかったのか。ここで出発点となる超越演算は乗法群(Multiplicative Group)の大源流たる「Inf(inity)/Inf(inity)=1」の方ではなく加法群(Additive Group) の大源流たる「Inf(inity)-Inf(inity)=0」の方なのである。そして、かくしてこれを起源に符号の正負が生じてめでたく世界が二分される訳なのである。


デカルト座標上では直線y=0を軸線に選ぶとxの値が+1から-1(-1から+1)にかけて推移するのに対して、yの値は決して0以下(0以上)にならない。見え方としては反時計回り。円関数集合(Circle Function Set)でいうとCos(θ)+Sin(θ)iに該当する。

同じくデカルト座標上で直線x=0を軸線に選ぶとyの値が+1から-1(-1から+1)にかけて推移するのに対して、xの値は決して0以下(0以上)にならない。見え方としては時計回り。円関数集合(Circle Function Set)でいうとSin(θ)+Cos(θ)iに該当する。


だがこの時点でその問題が直ちに表面化してくる訳ではない。デカルト座標系に到達するには、まだまだ段階を重ねなければいけないのである。

この式をさらに(無限小も無限大も含まない形に)一般化したのがCos(θ)+Cos(θ-SVoD)(Simple Vibration on Diameter=0→4)の形で、関数y=x/y=-xの共益関係(Conjugated Relationship)に立脚する円錐座標系(Conical Coordinate System)との関係がより明瞭に見て取れる。そしてここで回転する円盤に見えているものに正規分布(Normal Distribution)を射影すると相関係数関数(Correlation Coefficient Function)と重なってくる訳である。

ところで以前、自然指数関数(Natural Exponential Function)や自然対数関数(Natural Logarithm Function)を添字に対してひたすら入れ子にし続ける実験を試みました(3回目でほぼ収束)。今から思えばその結果はLp空間との何らかの関係を暗喩していたのです。
対象として単位円(Unit Circle)を選択する。
自然指数関数の添字化1回目
自然指数関数の添字化2回目
自然指数関数の添字化3回目(ほぼ収束)
自然対数関数の添字化1回目
自然対数関数の添字化2回目
自然対数関数の添字化3回目(ほぼ収束)
「 無限小<x<無限大と置く座標系」といえば、以下も巻き込む事が出来そうです。
直線と、その直線上に含まれない点Fを取る。
- 点Fから直線に垂線を下し、点Fのある方向が正と定めそれをx軸と考える(すなわち自明の理として直線が軸に定まり原点{0,0}を得る)。
- 直線上で点M'を動かすとき、その直角位置上でFM : MM'=e:1(e>0)を満たすような点Mの集合が円錐曲線を描く。この時FMとMM'の比の値eを離心率といい、直線を準線(Directrix)、 点 Fを焦点()という。
準線を共有する、いくつかの離心率eに対応する円錐曲線
焦点を共有する、いくつかの離心率eに対応する円錐曲線
- 0 < e < 1: 楕円
- e = 1: 放物線
- e > 1: 双曲線
なお、この方法で円錐曲線を描画した際、正円は現れない。これが円錐曲線に正円を含まないことがある由来になっているのだが、数学で円錐曲線を考える際は、便宜上e=0であるとき円を描くとされる(実際は点となる)。あるいは、準線と焦点を無限に離した極限で円になると考える。
放物線は二次曲線の一種で離心率(Eccentricity)=1である。
- 焦点(Focus)(0, c)、準線(Directrix)y =-cの時は放物線式x^2=4c*y(y=x^2/4c)。
- 焦点(c, 0)、準線x=-c の時は放物線式 y2=4cx(y=sqrt(x*4c))。
- 二次関数y=ax^2+bx+c(a≠0)が描くグラフは放物線になる。
年内どこまで進めるか分かりませんが、とりあえず「自分には数理が足りない」と自覚して再勉強を始めて2年目の到達点がこの状態という話…









