【数学ロマン】コンピューター時代の「色即是空空即是色」？

今年に入ってからやっと般若心教における「色即是空空即是色」の境地が数理に表せる様になってきた気がします。

• 我々の脳内もしくはコンピューター上で走る「数理三昧の世界」は「相応の有意水準設定と次元抽出を経た」現世=(全てが個別要素だけ切り出して論じる事が困難なt連続状態に置かれている)縁起世界の観測結果集合(Observation Result List)と演算結果集合(Observation Result List)の重ね合わせにのみ立脚している(そう運営されてない思考様式は「数理三昧の世界」とはいえない)。
  
• もちろん現世=縁起世界は我々の「視野内にある/視野外にある」に関わらず実存し、変遷を続け、その影響が「数理三昧の世界」の立脚する観測結果集合に及ぶ事もある。保守作業が間に合ってない箇所も当然出てくるだろう。だから少なくとも自分の小さな「数理三昧の世界」に立脚する発言は、ポパーの反証性理念やヴィントゲンシュタインの「語り得ない物については沈黙しなければならない」定理などに照会して慎重に行うべきである。
  
• 逆に「数理三昧の世界」における諸概念の影響が思わぬ形で現世に及ぶ事もある。例えば近世における指数関数的増大の概念の発見は(新世界作物普及に伴う人口の急増と結び付けて考えられ)マルサス「人口論(An Essay on the Principle of Populatio,1798年)」に代表される悲観的人口爆発論(それを戦争や災害の被害や疫病流行が未然に防いでいるとする)を生み出し、フランス革命からナポレオン戦争の時代(下手をしたら「太陽王の時代」をも含む)における虐殺合戦を加速させた可能性が指摘されている。さらにはガウスらが天体観測の精度を上げる為に磨き上げた「測定誤差を切り捨てノイズを下げる統計学的技法」にも(西洋の相対的没落や産業革命以降の貧富格差拡大を伴う資本主義的発展と結び付けて考えられ)「世界最終戦争論」登場の背景となった経緯がある。「(過度の悲観や楽観からの解放を目指す)数理三昧の世界」の運営者の一人を自認するなら、少なくとも自分くらいはそういう波及効果から自由でいたいものである。
  

いわゆる「ポリコレな人達」の行動現流を分析するに、概ねこんな感じで自らの「数理三昧の世界」を暴走させている人が多い様に見受けられます。

• まさに自らを「縁起世界の視野範囲外」からやってきた「認識可能範囲外を跋扈する絶対他者」と規定し「復讐」に加担したがる。
  
• その一方で主要分析手段が「分散の多次元性を直視する多変量解析」に推移したパラダイムシフトには乗り遅れ「(究極的には「世界最終戦争論」に行き着かざるを得ない)測定誤差を切り捨てノイズを下げる画一化志向」に執着し続けている。
  ＊何度でも繰り返すが、この件について大数の法則から正規分布概念を導出したガウスに罪はない。彼はただ天体観測の精度を上げたかっただけで、この場合最終的に正解となる座標はただ一つ、すなわち観測結果集合が「最大値=平均=最小値」となる事を想定するのは自明の場合だからである。問題は誰がその考え方を元来多次元的で分散幅があって当然の人間社会に適用しようと考えたかで、その結果がナチス的優生主義や最終戦争論に行き着いてしまうのである。
  

  ＊皮肉にもしばしばナチス的優生主義の祖に仮託される「ゴビノー伯爵の人種エントロピー論」は真逆の考え方で「人種の発展には混血による活気が不可欠だが、それが推し進める人種的均質化は最終的に人類を活気に欠ける熱的死状態に追い込んでしまう」ジレンマに素直に戦慄する立場なのである。これに比べればフランス構造主義の始祖の一人レヴィ＝ストロースが最終的に到達した「民族的独自性を守る為、文化混合は可能な限り回避すべきである」なる純血主義は現実の半分しか見ていない。「ゴビノー伯爵の人種エントロピー論」に拠れば、それもまた停滞の一形態に過ぎないからこそ絶望感が深まる訳である。そして人類はまだ、この問題提起に最終回答を得てはいない…
  

こうしたジレンマを回避するにはどうしたらいいか考えるのが今年の課題…そう、目指しているのはあくまで「何も分かってない時、何をすべきか分かるのが大人」の世界…

 以下のソースはこちら。

以前の投稿では複素数列SVoI(Simple Vibration of Imaginal=虚数単振動)Αn(n=1⇄-1)と複素関数e^iθの関係を探るうちに虚数共役(Imaginary Conjugate)に対応する実数共役(Real Conjugate)の概念に邂逅しました。元来は二つ合わせて複素共役(Complex Conjugate)概念の筈ですが、コンピューターの挙動に怪しい箇所が…

さすが複素関数分野の独習には参考書導入が不可欠です。

①オイラーの公式を用いるとコサイン波とサイン波をe^θiとe^(-θi)で表せます。
e^θi=cos(θ)+sin(θ)i(2-0)
e^(-θi)=cos(-θ)+sin(-θ)i=cos(-θ)-sin(θ)i(2-1)

②コサイン波の場合は…
e^θi+e^(-θ)i=2cos(θ)=(e^θi+e^-θi)/2(2-2)

③サイン波の場合は(2-0)式より(2-1)式を引いて2iで割ります。
(e^θi-e^-θi)/2i(2-3)

④複素数の極形式も次の様に指数関数で表せます。
a+bi=r(cos(θ)+sin(θi))=re^iθ

⑤また複素共役は以下となります。
a-bi=r(cos(θ)-sin(θi))=re^-iθ

⑥ピタゴラスの定理はこう表されます。
cos(θ)^2+sin(θ)^2
=(e^2θ+2(e^iθ×e^-iθ)+e^-2θ)/4-(e^2θ-2(e^iθ×e^-iθ)+e^-2θ)/4
=4(e^iθ×e^-iθ)/4=1

 どうやら「対称的なものと交代的（反対称的）なものに分解するための恒等式」x=(x+y)/2+(x-y)/2と密接な関係にある様です。

①任意の行列は対称行列と交代行列の和に分解可能である。
A=(A+At)/2+(A-At)/2

②任意の関数は偶関数と奇関数の和に分解可能である。
f(x)=(f(x)+f(-x))/2+(f(x)-f(-x)/2

③任意の2変数関数は対称式と交代式（反対称式）の和に分解可能である。
f(x,y)=(f(x,y)+f(y,x))/2+(f(x)-f(y,x))/2

この考え方を援用すれば、指数関数e^xも，偶関数と奇関数の和で表せます。
e^x=(e^x+e^−x)/2+(e^x−e^−x)/2

実は右辺の偶関数部分はカテナリー(懸垂線)と呼ばれる有名な曲線です。偶関数の部分はcoshx、奇関数の部分はsinhxとも表され，双曲線関数とも呼ばれます。

さらには、以下の関数の挙動も取り込んでいかないといけません。

実数関数y=(1+0i)X^nの場合(第一象限の虚数部が動かない)

複素関数y=x(0+1i)^nの場合(実数部と虚数部の交代が起こる)

実数関数y=log(n,(1+0i)x)の場合(第一象限の虚数部が動かない)

複素関数y=log(n,(0+1i)x)の場合(実数部と虚数部の交代が起こる)

なるほど、これまで実数共役(Real Conjugate)の概念を私の視野から隠してきたのは、この「第一象限の実数関数では虚数部が動かない(第四象限の動きも異なる。第二象限と第三象限の動きは同じ)」なる振る舞いだったのです。そして指数関数Y=X^Nの実数部の挙動はマクローリン級数(McLaughlin Series)による近似過程そのままです。

さて、こうした話は何処へ収束(Convergence)していくのでしょう？

そもそも×(0±1i)とは？

とりあえず上掲式が処理過程でどう見えるかプログラムでも確認していきましょう。まずはガウス平面(Gaussian plane) 上で(0±1i)を掛ける事にどういう意味があるか確かめる必要がありますね。これ自体は簡単。ガウス平面上において座標を実部中心に±90度回転させるのです。

Cos(θ)の正体?

とりあえず上掲式が処理過程でどう見えるかプログラムでも確認していきましょう。まずはCos波の計算過程を式そのままに図示してみると、ただでさえ距離が足りてない上(端が欠ける)、e^θi+e^-θiに対して「中心{0,1},半径2の円弧のcos(θ)」を、(e^θi+e^-θi)/2に対して「中心{0,1/2},半径1の円弧のcos(θ)」を返してきます。

e^θi+e^-θi

(e^θi+e^-θi)/2

添字にπ/2を掛ける事によって初めて見慣れた円状分布(Circular Distribution)が現れるのです。

e^(θi×π/2)+e^(-θi×π/2)

(e^(θii×π/2)+e^(-θii×π/2))/2

Sin波の正体

Sin波の場合もやはり、計算過程を式そのままに図示すると距離が足りていません(端が欠ける)。

e^θi-e^-θi

(e^θi-e^-θi)/2(0±1i)

やはりこちらも添字にπ/2を掛ける事によって初めて見慣れた円状分布(Circular Distribution)が現れるのです。

e^(θi×π/2)-e^(-θi×π/2)

(e^(θi×π/2)-e^(-θi×π/2))/(2*(0±1i))

オイラーの定理e^πi=cos(θ)+sin(θ)iから円状分布(Circular Distribution)の世界へ

とはいえ、こうして得られた円状分布(Circular Distribution)は、cos(θ)の場合に0→1→0、sin(θ)の場合に-1→0→1と推移してしまいます(見慣れたcos(θ)/sin(θ)の振る舞いだと第四象限から第二象限に掛けての振る舞い)、とはいえ両波形は位相が90度(π/2ラジアン)ズレてさえいればセットで無限周期で円を描き続けるので、どうとでも調整が効く次第。

• cos(θ)=±(1-abs(sin(θ))
• sin(θ)=±(1-abs(cos(θ))

こういう対応関係も利用可能です。

むしろ気になるのは、これだけ選択肢があり、かつ明らかに語源的には正弦波(Sine Wave)あっての余弦波(Cosine Wave)だったにも関わらず、歴史的にはいつの間にか立場が逆転しまった流れ。

• 最初の契機として想定されるのが、マクローリン級数による近似を出発点としてのオイラーの定理e^πi=cos(θ)+sin(θ)iの発見。以降cos(θ)は偶関数、sin(θ)は奇関数の代表例と目されていくが、マクローリン級数による近似ではまず偶関数が最初に現れるのである。
  
• 次の重要な契機として想定されるのがガウス平面(Gaussian Plane)の制定で、この時点までに既に完全に(Cos(θ)によって表される)X軸上の実数部が主、(Sin(θ)iによって表される)Y軸上の虚数部が従として動くイメージが樹立していたと想定される。
  

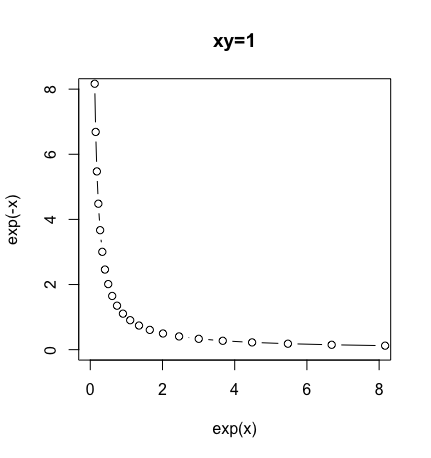
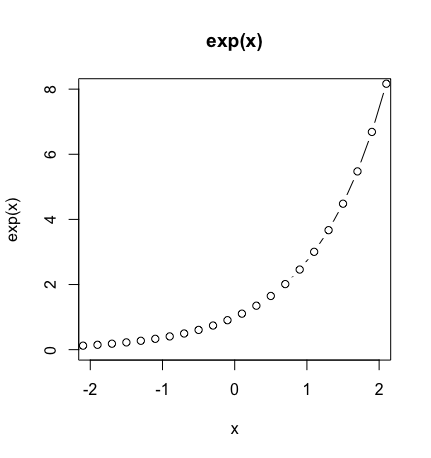
脱線が過ぎました。それはそれとして、透視図法に対応する自然指数関数(Natural Exponential function)や自然対数関数(Natural Logarithmic function)の概念、すなわち「xy=1(面積)となる数列の積の極限」がピタゴラスの定理(Pythagorean Theorem)z^2=sqrt(x^2+y^2)と関係してくるのが、なんとも不思議な感じがします。

さらに奇異に感じるのが「X軸が奇数系でY軸が偶数系」の以下の方眼。

で、とっさに思いついたのが(しばらく前から使い始めた、角度の概念を放棄した)円状対数尺(Circular Logarithmic Scale)だったという次第。要するに共役(Conjugate)概念の全周化…

どうやらe^xが幾ら微分しても、幾ら積分してもe^xのままである事と何か関係がありそうです。

そして、以下からのソースはこちら。

この機会に以下の投稿で得てきた知見をまとめます。

ポイントとなるのはこの考え方ですね。

三角関数の微分（それぞれが-90度の変遷に対応）
Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)→Cos(θ)
Sin(θ)→Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)

三角関数の積分（それぞれが+90度の変遷に対応）
Cos(θ)→Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)
Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)→Sin(θ)

対応する自然指数関数の90度位相変遷
-90度（微分）方向…>exp(θi)→log(θi)→-exp(θi)→-log(θi)→exp(θi)
+90度（積分）方向…exp(θi)→->log(θi)→-exp(θi)→log(θi)→exp(θi)

対応する自然対数関数の90度位相変遷
-90度（微分）方向…log(θi)→->exp(θi)→-log(θi)→exp(θi)→log(θi)
+90度（積分）方向…log(θi)→exp(θi)→-log(θi)→-exp(θi)→log(θi)

合算すると以下の様に見えます。 
三角関数と自然指数・対数関数の巡回性
元関数(微分0回目)e^(θ×(0±1i))=cos(x)+sin(x)×(0±1i)

微分1回目log(θ×(0±1i))=-sin(θ)+cos(θ)×(0±1i)

微分2回目-e^(θ×(0±1i))=-(cos(x)+sin(x)×(0±1i))

微分3回目-log(θ×(0±1i))=-(-sin(θ)+cos(θ)×(0±1i))

微分4回目e^(θ×(0±1i))=cos(x)+sin(x)×(0±1i)(最初に戻る)

あれ微分しても積分しても同じ形のe^xは何処に？

それについてはこんな話もある様です。

マクローリン級数によるオイラーの公式e^ix=cos(x)+sin(x)iの「証明」の問題点（e^ixの定義はどこに隠れているか） を指摘する朝永振一郎のエッセイを紹介します．

朝永振一郎(1906～1979,ノーベル物理学賞を受賞した日本を代表する物理学者）は，エッセイ ｢数学がわかるというのはどういうことであるか｣ （朝永振一郎 『科学者の自由な楽園』 江沢 洋(編集) 岩波文庫，2000 に所収） において，オイラーの公式と出会ったときのことを次のように記しています （中学とあるのは旧制中学で卒業は17歳）。

幾何学的に定義された三角関数というものが、 指数関数という解析的なものと結びつくということは何とも脅威であったが、 それだけにまたその意味が理解できない、 証明はベキ級数を使ってやればいかにも簡単明りょう疑う余地はないが、 何かごまかされたみたいで、あと味が悪い、 ところが、やはり中学生より大きくなっていたので、 そのあと味悪さの原因がどこにあるかに気づいた。 どう気がついたかというと、この定理が出てくる前に、 数の虚数ベキの定義がやってないという点である。 ベキの定義はまず正の整数ベキから出発し、次に負数ベキが逆数と関係させて定義され、次に分数ベキが平方根とか立方根とかに関係させて定義されている。 ここまでは中学校で教えられた。さらに進んで無理数ベキは極限概念として微分学で習っている。ところが虚数ベキの定義になると、まだどこでも習ったことはない。 その習っていないものがいきなり式の左辺に出現したのだから理解できないのは当然である。 そういうことに気がついた。こう気がつくと、この定理の意味は一目りょう然となった。 つまり、これはむしろ虚数ベキの定義そのものなのであると、やはり高校生になると中学生のときとちがって、もやもやとわからないといっていないで、なぜわからないか、どこがわからない原因かと、つきとめることができたのであろうか。

虚数ベキe^ixの定義こそが問題であると指摘されています。指数関数のベキ級数展開e^xにおいてxをixに置き換えた式をe^ixの定義とするとオイラーの公式が導かれるという証明になっているからです(無限級数の収束、実部と虚部に分ける順序交換は絶対収束級数であることから正当なものです）あるいはオイラーの公式e^ix=cos(x)+sin(x)iをe^ixの定義とする方法もあります（オイラーの発見を尊重しない悪いやり方だという人もいますが， 数学ではよくやる手段です）。

そもそもe^x関数でcos(x)と合成されているのはどんな波形なんでしょうか？

現れたのはSinh関数…

それと対になるのはCosh関数…

以下のソースはこちら。

残された問題は「どうしてe^xiとe^-xiの平均を求めると(X軸上のCos波やY軸上のSin波といった)円状分布(Circular Distribution)を構成する材料が得られるか」だけとなります。しかし考えてみれば自然指数関数の正体は「0を中心に-InfからInfを直線で結ぶ均等尺を1を中心に0からInfを結ぶ直線に射影して現れる対数尺」な訳ですから、この演算自体に(等差数列上の)1単位の均等尺を(等比数列上の)ネイピア数単位の対数尺に変換する効能があり(現時点の私はこの数理自体の詳細を全く知らない)、(0±1i)方向へのπ倍のベクトル入力により円形性(Circularity)を取り戻すとでも考えるしかないのです(それがまさに自然指数関数Cosh波とSinh(θ)波にオイラーが加えた操作だった訳だが、むしろこの操作が数理構造全体において如何なる意味を持つかが、私が知る限り未解明のまま)。

以下のソースはこちら。

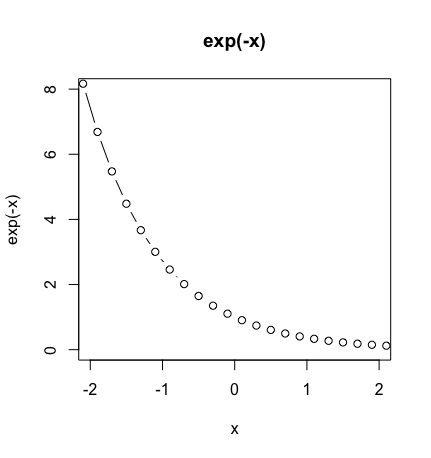
そんな感じで以下続報…