Wikipediaの「ヒルベルト空間」の説明を読んでもさっぱり頭に入ってきません。
こういう時は「非数学者」の意見を参照するに限ります。
ベクトル空間
とりあえず,ベクトルが定義できる空間を考える.ここで我々が想像しやすい3次元空間を思い浮かべるかも知れないが,空間と言っても数学的な意味での空間なので気をつけよう.つまり,様々なベクトルの一つ一つが要素であるような集合のことを言っているのだ.ここで言うベクトルは何次元だって構わない.
そして,このベクトルの間には加算が定義できて,交換法則,結合法則が成り立ち,スカラー倍の計算が定義され,零元,逆元が存在するとする.まぁ,普段当たり前だと思っている計算がちゃんと出来るということだ.
- この辺りを私は「形相(Eidos/ Form)=その前提なしには数集合を等比数列や等差数列に表す事も出来ない規約」と理解し、まずは自然数集合(Natural Set)と加法整数群(Additive Integer Group)の概念をそれに分類。
- さらにはこれらを「互いに直交するN次元座標軸」として配置した「前後/上下/左右を峻別する」デカルト座標系(Cartesian Coordinate System)概念も(視覚とそれを処理する脳を備えて以降、生物の認識系に先験的(A Priori)に超越的(Transcendental)に実装される様になった)形相に分類すべきかもしれない。近世以降の数理はむしろ極座標系(Polar Coordinate System)を再出発地点としてデカルト座標系を前提に蓄積してきた知識を再吸収する道を選んだといえよう。それでも過去の遺物と化さない辺りに、この概念の形相としての強固さを偲ばせる。
こういうのを「ベクトル空間」という.まだヒルベルト空間ではない.
座標原点からさまざまな方向に伸びるさまざまな長さのベクトルが定義できるという映像を想像するといかにも空間を張っているみたいだろう.ここへ来て数学による抽象的な表現と我々の具体的な「空間」のイメージが重なるわけだ.
内積空間・ノルム空間
さらにベクトルとベクトルの間に内積という演算が定義できるとしよう.ここで高校で学ぶ内積を思い浮かべるかも知れないが,まぁそのイメージでいいだろう.数学的には幾何学でやった内積と同じものをその計算式だけで定義してやって,これを内積とする,という回りくどい定義の仕方をする.それが出来る空間を「内積空間」あるいは「プレ・ヒルベルト空間」と呼ぶ.
- 一辺1の正方形の平方対角線(Square Diagonal)の長さがsqrt(2)(1.414214)となり、一辺1の立方体の立方対角線(Cubic Diagonal)の長さがsqrt(3)(1.732051)と無理数(Irrational Number=有理数の様に比で表せない数)になるので整数(Integer)を神聖視する古代ギリシャの数学者が追求を諦めてしまった事で有名な分野。(ユークリッド幾何学やプトレオマイオスの数論といった)ヘレニズム数学には早くもそれからの脱却を図る動きが見られるが(本格化するのはむしろアラビア数学の段階において)、複式簿記の記法と併せてそれが欧州に本格導入されるのはルネサンス期出版革命を迎えた近世以降となる。
上掲の様に自然数集合や加法整数群の定義に用いた等差数列(Arithmetic Progression=算術数列)概念を「元の数集合を特定の数で割った剰余に注目する」剰余群(Quotient Group)に拡張し数集合族(Family)の任意の元(Element)が全て1対1で添字集合(Index)に対応する範囲に注目すると、数集合を添字化(Indexing)と単位化(Unitization)の入れ子構造で表し2進法(Binary System){0,1}や10進法(Decimal System){0,1,2,3,4,5,6,7,8,9}による(小数点下を含む)桁管理を導入する事により「自然数概念、整数概念の次に有理数概念や無理数概念を追加する」と考える伝統的数直線原理主義(Traditional Number line Fundamentalism)の拘束から脱却する事が可能となる。
ちなみに無理数についてはコンピューター演算に採用されている様に「必要精度まで計算して以下は誤差として切り捨てる。切り捨てた誤差が問題となる場合には計算精度そのものを見直す」方針を採用。古い数学入門書はしばしば「ある数を3で割って3を掛けた結果(1/3*3=0.9999…)」と「ある数に3を掛けて3で割って結果(1*3/3=1)」が食い違う事を「コンピューターが人間の知性に劣る決定的証拠」に挙げてきたが、この欠陥を克服する(Yacasの様な)代数ライブラリが代わって広まる事はなかった(それが必要となる状況が限られ過ぎている)。むしろ、かかる誤差問題は「必要なだけ計算を進め、剰余項を誤差として示す」テイラー級数(Taylor Series)/マクローリン級数(McLaughlin Series)やフーリエ変換(Fourier Transform)の時代から数理の本質として実存してきたのであり、ガウスが誤差関数(ERF=Error Function)や相補誤差関数 (ERFC=complementary Error Function) を発明して「必要精度まで計算して以下は誤差として切り捨てる。切り捨てた誤差が問題となる場合には計算精度そのものを見直す」方針を発表して天体観測の分野に歴史的画期をもたらしたと考える方が私の目指す「数理三昧の世界」らしい展開といえよう。
- かかる思考様式は欧州への複式簿記の記法概念導入を契機に始まった筈だが、会計処理が小数点下の処理を嫌う為、(伝統的背徳感が克服され)利率演算(Interest Rate Operation)の概念が普及するまで軍事や建築や(透視図法概念と関係してくる)美術といった「一般人の視野に入らない分野」でこっそり用いられてきたに過ぎなかった。これは(長い間「賭博師の技」と貶められてきた)確率演算(Probability Operation)概念も同じで、自然指数関数(Natural Exponential Function)や自然対数関数(Natural logarithm Function)の概念は奇しくも近世欧州におけるそれらの統合過程で「前代未聞の発明」として登場してくるのである。
- どうやら「添字付集合(Indexed Set)」の概念自体は、群論でいうと全単射(Bijection) の概念に対応する様だが、説明が難しくて断言までは出来ない。説明が難しいのは概ね例外を想定しているからで、実際その実例に遭遇したらこの定義は加筆される事になる。
内積が定義できると,直交とか,ノルムとかいう概念が定義できるようになる。例えば2つのベクトルの内積が0になる時を直交という.これは幾何学のイメージからそう呼んでいるだけだ。
そして,ノルムというのはベクトルの自分自身との内積の平方根を取ったものである.すなわち,ベクトルの長さのようなものだ。
ではなぜわざわざ「ノルム」と呼んで「ベクトルの長さ」と言わないのかというと,数学では全てを抽象的な概念でまとめて扱う.この手続きがいつも私たちが知っている「長さ」を意味するとは限らないのである。
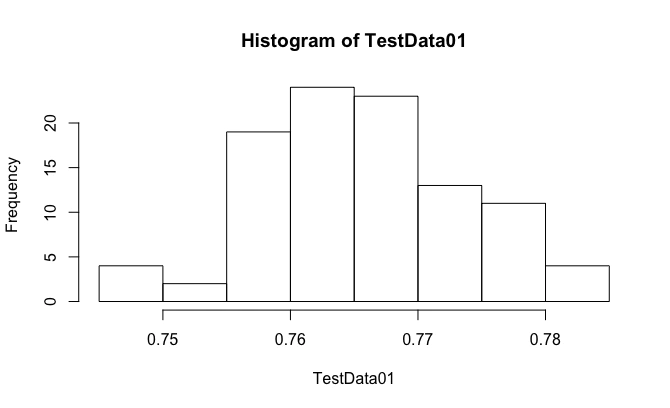
- 例えば距離関数(Distance Function)の一つpノウム演算(x^p+x^p+x^p…)^(1/p)は、確率統計学や機械学習の分野において観測結果集合(Observation Result Set)について「集計内容が距離に該当する場合の、集計に先立っての各データの数値最適化」に用いられる。この辺り、度数分布表(Frequency Table)の一種であるヒストグラム(Histogram)を正しく用いる為のテクニックと重なってくる。それ自体は結構「匠職人の世界」というか「可算直積可能な数理世界」からのみのアプローチでは最適化が困難で、だから確率統計学や機械学習に出番が回ってくるイメージ。
- ノルム空間成立の第一条件は「‖x‖=0⟺x=0」すなわち「空ではない観測結果集合の数だけ零元が存在する事」。第二条件は「‖ax‖=|a|‖x‖」すなわち「(添字付集合の形での表現が可能で)スカラー倍の計算が定義される事」。今年に入ってから上掲の近代以降に成立した数理的諸概念(Mathematical Things)を「オイラー座標系(Eulerian Coordinate System)」なる一貫した言述(Discours=ディスクール)に統合する試みを始めたが、とりあえず既に上掲2条件は既に満たされている。
第三条件の「‖x+y‖≦‖x‖+‖y‖」すなわち「三角不等式の成立」についてはオイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)における「(NoS=0)」「確率統計段階(Probability Density Level, NoS=0以上2未満。おそらく素数2^0族の世界。辺と呼べる対象が1本ずつしか存在し得ず、しかも任意の円の中心から円弧に伸ばした線は全て直交するので内積0)」と「整数直線段階(Integer Line Level,NoS=2。おそらく素数2^1族の世界。‖x+y‖=‖x‖+‖y‖の空間なのでやはり内積0)」の場合についてはまだ言及の余地がなかった。これからの課題といえよう。
ところで先ほど,「内積が定義できるとノルムが定義できる」と書いたが,実は内積が定義できなくてもノルムの定義自体は出来てしまう.ここでは定義は書かないが,そういう空間を「ノルム空間」と呼ぶ。
完備性
さて「ヒルベルト空間」はまだなのかと待っていることと思うが,ここまでの話にもう一つ条件を加えるだけでいい。
バナッハ空間については今回の話とは関係ないが,まぁ,数学ではこんな具合に分類されて名前が付いているんだよ,という雰囲気をつかめるように書いておいた.
な.物理学者は「ヒルベルト空間」なんて言葉でカッコつけなくてもいいんだよ.他の数学的空間の性質と区別する必要があるときにだけ使えばいいんだからさ.
- そもそもLp空間を構成するpノウム演算と内積の概念の並立は困難である(係数ごとに変化する2点間の距離に注目している時、その線上にない任意の第三点を置いてそれとの関係を計算するモチベーションを想定する事自体が難しい)。これは(そういえばこれも距離関数の一種と見做せる)オイラーの等式(Eulerian Identy)(1±πi/N)^N=-1も、Nを1から無限大(In(finity))に推移させていく過程で計算上の終点の位置を{1,π}から{-1,0}に連続的に変化させていくが(始点との距離はπから2に推移)、やはりここに線上にない任意の第三点を置いてそれとの関係を計算する意義を見出すのが難しいのである。一方でどちらもコーシー列はきっちり構成する事が見て取れ、という事はパナッハ空間だという事?
- 実際のオイラーの公式(Eulerian Formula)(1±πi/N)^N=に代入するのは任意の数値で良く、その数値によって与えられた座標を回転させる。
四元数(Quaternion)の正規部分解表現(Sympletic Form)に該当。で,気になっていることと思うが,「完備性」とは何だろうか.
コーシー列が収束する時,完備性を持つのだそうだ.ではコーシー列とは何かと言えば,集合から好きな要素を取り出して並べた時に,あるところより先の要素を見ると必ず,それらの要素間の距離がどんな狭い範囲にでも収まってしまう,そんなところが必ずある,という並びのことらしい.ああ!数学ってのは七面倒くさい!!!とにかく,どこまでも狭い範囲に収まって行くような並びのことだ.
それで,狭い範囲に収まって行くのなら収束していると言えるのではないか,というと,そういう意味ではない.例えば√2に限りなく近付くコーシー列があったとしても,この空間内に√2という無理数が定義されていなければ√2に収束するとは言えないわけだ.
- 私が現在編纂している「オイラー座標系(Euler Coordinate System)」なる概念は確立密度空間(Probability Density Space)と「名状し難きもの(The Unnamable)は名状し得る場合(Namable Case)、既にそこには存在しない。ならば名状し難きものものとは一体何者か?」 なるジレンマの組み合わせによってこの「収束先を名状する方法がない」状態を回避している。
この空間においては、そもそも観測結果集合(Observation Result Set)が空の次元は認識対象外となるが(上掲のノルム成立の第一条件)、それに説明が与えられない場合には一律「名状し難きもの(The Unnamable)」の分類に放り込んで、一旦は一切の判断の対象外とする。現実世界のオカルトの概念に対応?
数学的な表現はやめて,分かりやすく言い直そう.これはベクトルが連続であることを定義しているのである.この性質は微分などを定義するためには是非とも必要なものだ.そして,それはもっと分かりやすく言えば,このベクトルの要素は実数か複素数の範囲でなければならないという意味である.初めからそう言えよ,って?私もそう思う.
こんなもんなんだよ
なんだ,それだけか?結局,ぶっちゃけて言えば,「取り敢えずの計算に困らないベクトル空間」というくらいの意味だったということだ.実に他愛のない話だ.だからこそ一度知ってしまうと今度は逆に,これくらいは知ってないと恥ずかしいと思えてしまうわけで.
まあ,奥は深いのだが,これだけ知ってるだけでもしばらくは困らない.さあ,立場の弱い友達の所へ行って知ったかぶりをするのだ!(笑ま,この程度のものは黙ってた方が恥かかなくて済むかとも思うのだが,・・・判断はお任せしよう。
なるほど、とりあえずはこういう考え方でいいのか!! そんな感じで以下続報…