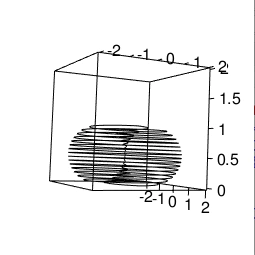
「無限量子井戸」とはこれ。
1次元無限井戸型ポテンシャルのシュレーディンガー方程式を解いて, 粒子がどのような分布をとるのかを見てみます。
取っ掛かりは以下の「観測者によってどちら向きに波紋が動いているか違って見える画像」でした。



よく考えてみると「利用されている座標集合」自体は共通しており、如何なる補助線も引かれてない段階でも実存している訳です。そしてその座標集合は以下では全く別物に差し替えられますが「人間の目に検出される座標集合」のみに注目すると、それほどの違いはないという考え方も出来る訳です。

線形的な量または線形的な幾何概念を一般化したもので、基底を選べば、多次元の配列として表現できるようなものである。しかし、テンソル自身は、特定の座標系によらないで定まる対象である。個々のテンソルについて、対応する量を記述するのに必要な配列の添字の組の数は、そのテンソルの階数とよばれる。
例えば、質量や温度などのスカラー量は階数0のテンソルだと理解される。同様にして力や運動量などのベクトル的な量は階数1のテンソルであり、力や加速度ベクトルの間の異方的な関係などをあらわす線型変換は階数2のテンソルで表される。
物理学や工学においてしばしば「テンソル」と呼ばれているものは、実際には位置や時刻を引数としテンソル量を返す関数である「テンソル場」であることに注意しなければならない。いずれにせよテンソル場の理解のためにはテンソルそのものの概念の理解が不可欠である。
ブルバキによる多重線型代数の再構成において、それまでの多重線型代数の一流儀であった四元数(より一般にはリー群との関係から導かれるような)を通じてテンソルを考える方法は打ち捨てられることになった。ブルバキが採用したのはより圏論的な方法論であり、普遍性をもとにした議論によって多重線型代数の理論は大きく整理された。 こうして、テンソル空間 を考えることによって多重線型性の問題が単なる線型性の問題へと言い換えられる、ともいうべき理解が得られた。この過程で用いられる操作は純代数的なものであり、幾何学的な直感は見かけ上完全に排除されている。多重線型代数の理論を代数的・圏論的に整理したことによって多重線型的な問題の「最適解」の概念がはっきりとしたものになる。その場その場に応じた、座標系を用いたりして幾何学的な概念に訴える必要無しに、すべてのものが「自然に」構成できることになる。
いずれにせよ、とりあえず私は(それ自体は観測不可能な)観測原点0と観測限界Infi(inity)の間に分布内容が未知の(というか、そもそも出発時点ではそれが常に全域に渡って均一だという保証もない)確率密度空間(Probability Density)を置き、それから得られた観測結果集合(Observation Result Set)が特定の演算結果を満たす時、それを演算結果集合(Operation Result Set)としても認めるという立場を採用しています。
そうして得られる演算結果集合を代表するのが実数軸(Real Axis)で、観測者がその積をどこまで認めるか(切り捨てるないか)によって零次元(0本)、一次元(1本)、二次元(2本)、三次元(3本)の違いが現れますが、それぞれの空間はそれとバーターにある種の視座(Perspective)制限を強要される展開を迎えるのです。
①点=同心円空間(Dot=Concentric Circle Space)0-0.5次元の広がりを有する2^0座標系の場合は全周範囲(2π Range)。
②線=円柱/トーラス空間(line=Cylinder/Torus Space)1-1.5次元の広がりを有する2^1座標系の場合は半周範囲(π Range)。
③デカルト座標系=円錐空間(Cartesian Coordinate System=Cone Space)2-3.5次元の広がりを有する2^2/2^3座標系の場合は1/4周範囲(π/2 Range)/1/8周範囲(π/4 Range)。
- ちなみに四元数(Quaternion)は2^3座標系とは2^1座標系からの拡張のされ方が異なる3^2座標系に分類される(それぞれが複素数平面を備える二つの回転軸の組み合わせにより全周範囲視座を回復)。
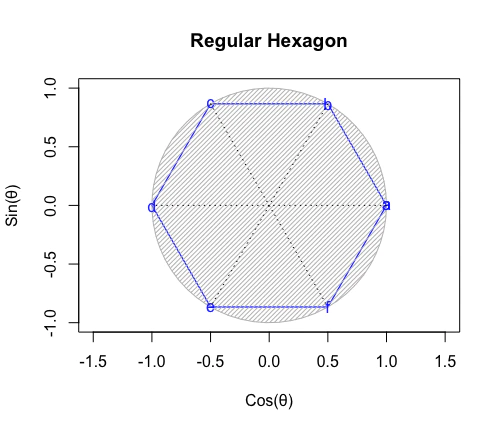
④いずれにせよ2^3座標系も3^2座標系も素数族2^n3^mの部分集合に過ぎず、平面上の正六角形(Regular Hexagon)による平面充填(Tiling)をその極限とする。
この座標系においてはオイラー標数(Eulerian Characteristic)すなわち凸多面体の頂点(Vertex)数をV、辺(Edge)数をE、面(Face)数をFと置いた場合のχ≡V-E+Fが次元によって異なると考えます。
①立体上におけるオイラー標数=2は「偶数系立体(Even-numbered Solid)=正多面体(Platonic solid=プラトン立体)でいうと正六面体(Cube),正八面体(Regular Octahedron),正12面体(Regular Dodecahedron),正20面体(Regular Icosahedron)」における(凸型正多面体の場合は単一となるその立体の)外接球面上の対蹠(Antipodes)の対、「奇数系立体(Even-numbered Solid)=正多面体でいうと正四面体(Regular Tetrahedron)」における(それぞれの対蹠を始点とし、特定の面を終点とする展開の対における)始点と終面に該当する。オイラーの多面体定理の証明を通じて得られるこのイメージは、関数における(逆関数を持たない)偶関数(Even Function)と(常に逆関数と一対で現れる)奇関数(Odd Function)の関係に対応する。
②一方、 平面上におけるオイラー標数=1と線上におけるオイラー標数=0は多辺形(Polylateral)/多角形(Polygon)の面数を表裏2面と数えるか(xyz座標系が実軸と認識される世界)、片側1面と数えるか(xy座標系が実軸と認識される世界)輪郭線のみに着目して0面と数えるか(数直線の様にスカラー量の増減のみが実軸と認識される世界)に由来し、この選択こそがまさにそれぞれ2.0-2,5次元と3.0-3.5次元、1.0-1,5次元と2.0-2.5次元の境界線となる。
ちなみに(線上もしくは平面上の)多角形において頂点数と辺数は必ず等しくなるが、オイラーの公式(Eulerian Formula)e^θi=cos(θ)+sin(θi)など(1の冪根に由来する)ガウスの巡回群を用いた計算ではこれに(始点と重なる終点、あるいは終点と重なる始点となる)原点1を加える。例えば統計言語Rにおける(円の近似たる)60角形の表現は
c<-seq(-pi,pi,length=61),x<-cos(c),y<-sin(c)となる。
ぶっちゃけ幾何学的世界観と統計学的的世界観を擦り合わせる為の方便な訳ですが(ここまで全体像がまとまるまで1年以上掛かった!!)、最近、次第にこの立場には確率微分方程式や統計力学や量子力学の世界に引き寄せられていく(最後には併合されてしまうのかもしれない)という問題がある事が明らかとなってきたのです。
さて、どうしたものか…