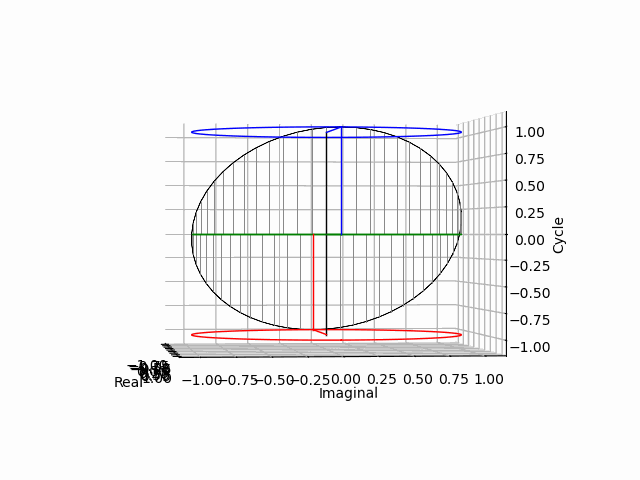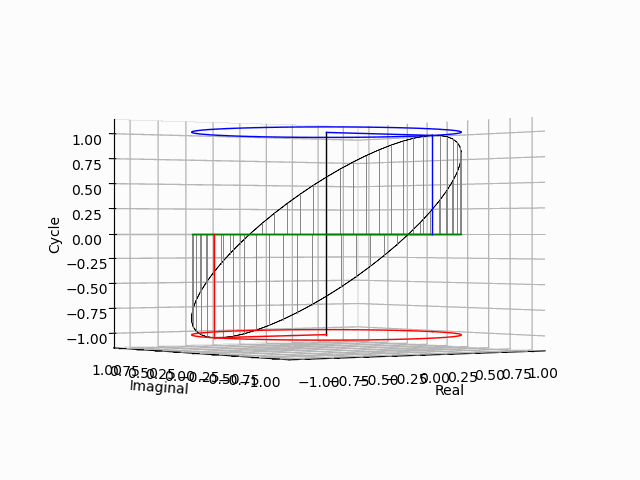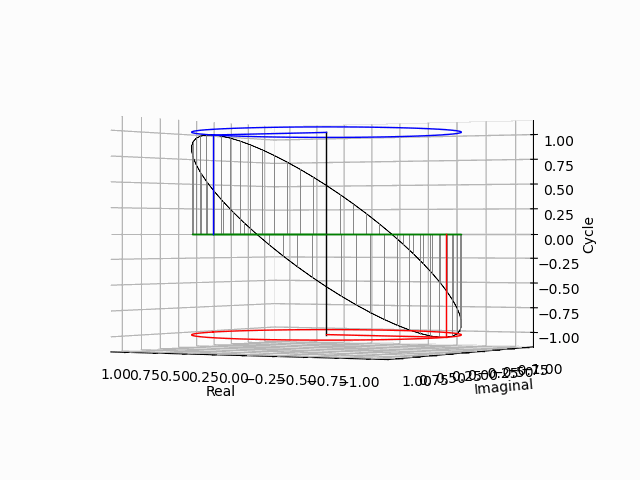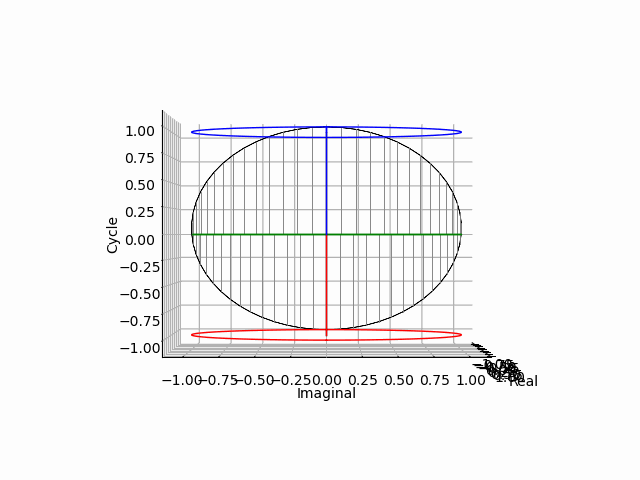
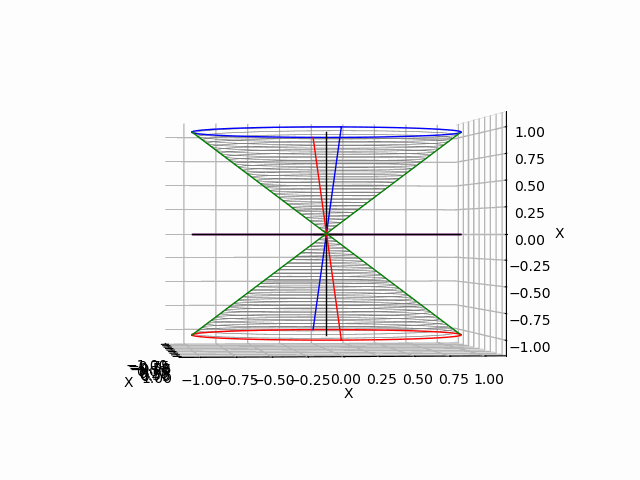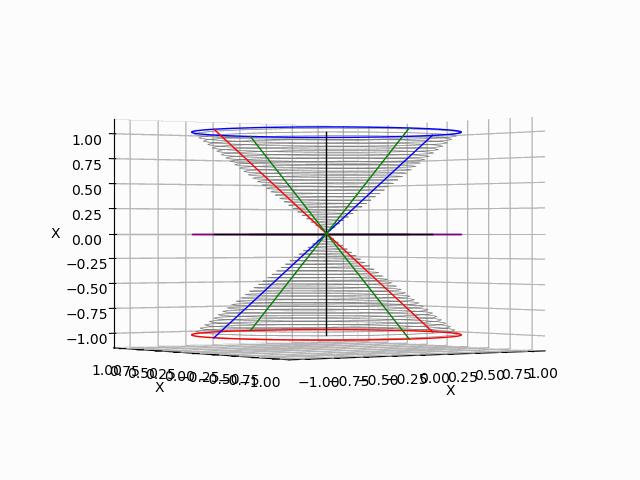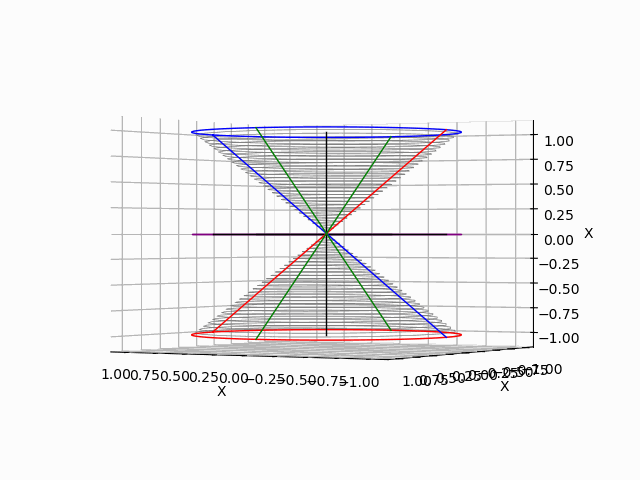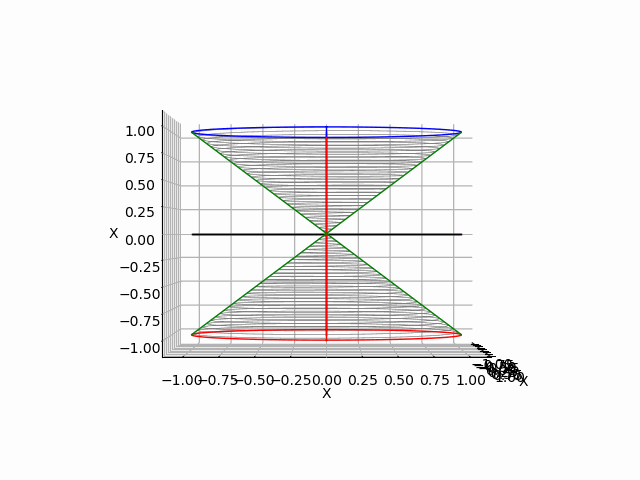
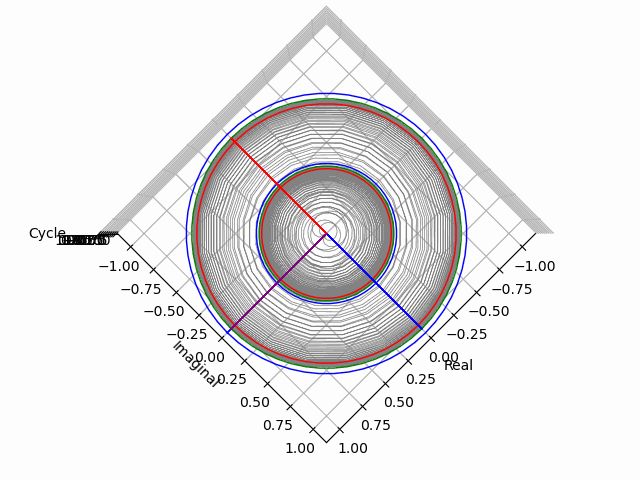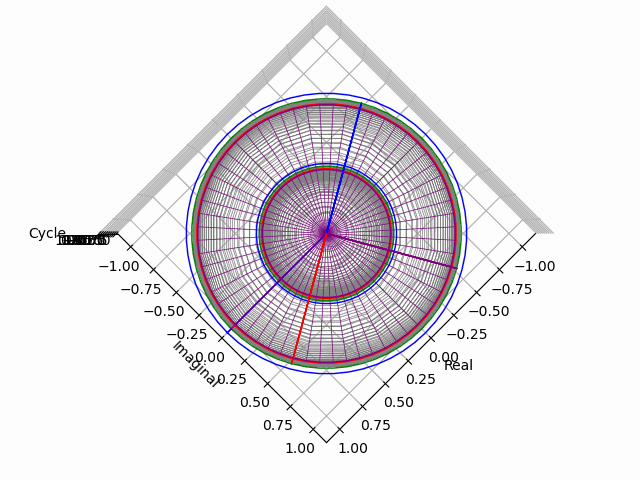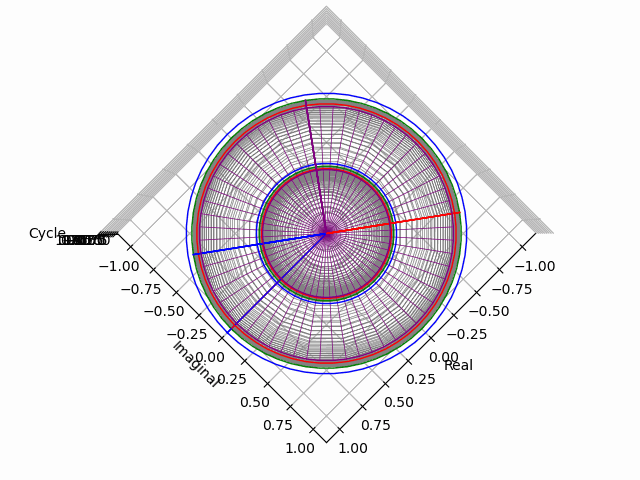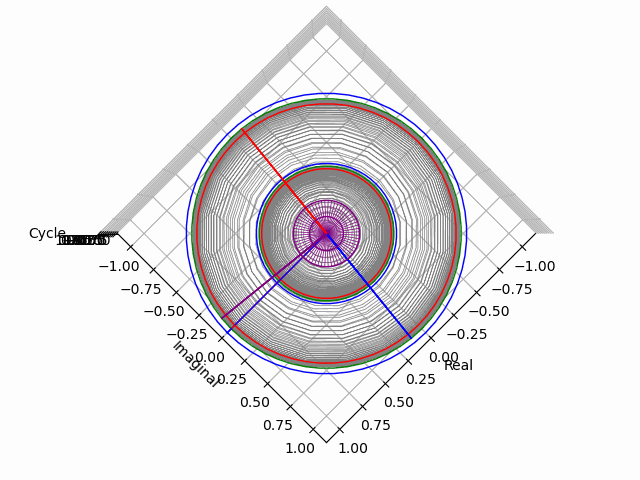
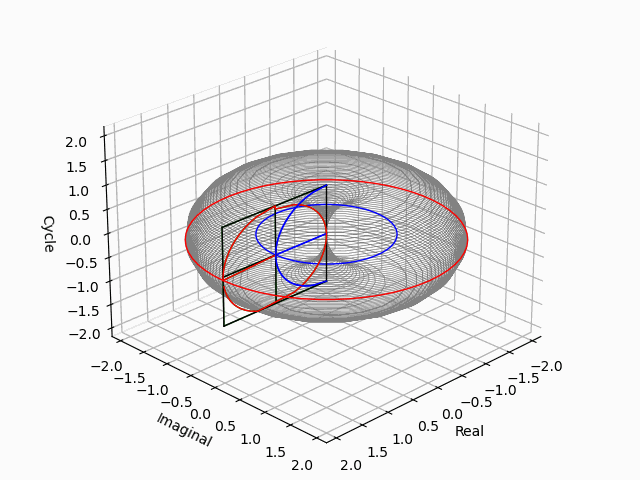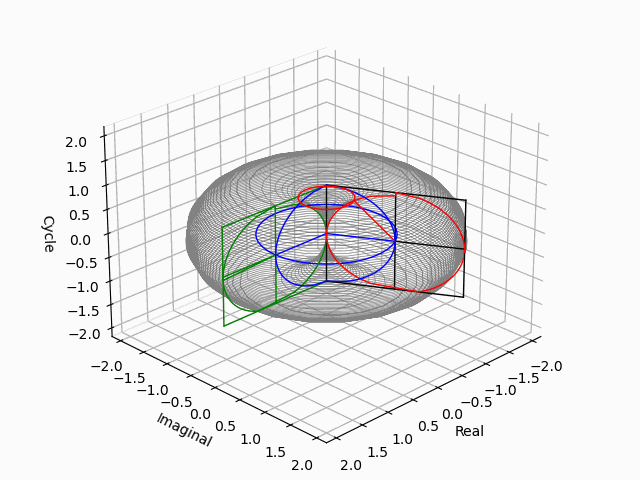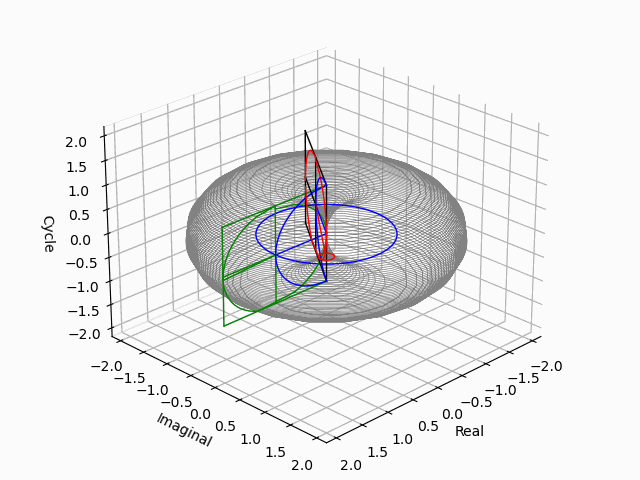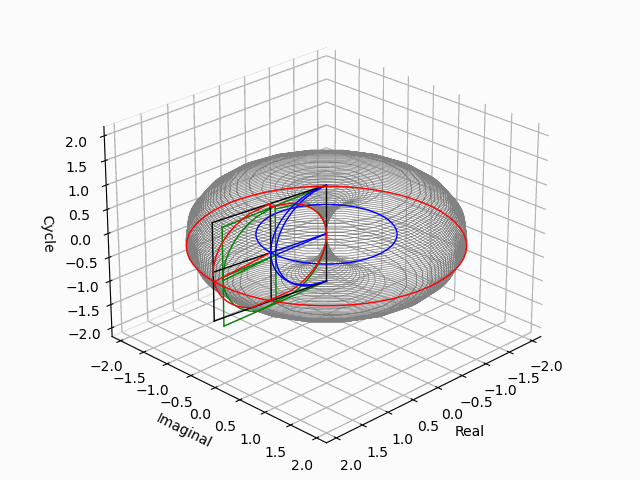
「垂直観察(Vertical Observation)=直行方向からの観察による次元削減」からの「削除された次元の内容の数理的復元」は基底抽出(Basis Extraction)における最も著名な手段の一つです。座標系(Coordinate System)との関係でいうと正面図は「奥行」、側面図は「幅」、上面図は「高さ」を省略した残余で「背面図」「逆側面図」「下面図」は観察方向の符号逆転バージョン。それぞれもう一回別方向からの観測結果を求めると線形集合が三個得られますが、陰線除去の観点から省略される次元も「各点の順序情報」や「回転情報」などは参照されます。

この「繰り返し残余を求める演算」は「N進数における桁振り演算」にも登場。

元来(その一次結合によって全体量を表せる)基底集合(Basis Set)の定義において重要なのは「互いに原則として無相関(Uncorrelated)である事(座標系によっては演算後の桁上がりや桁下がりがある)」なので、上掲の様に「幾何学上の直交概念と紐付けられたイメージ」を特に直交基底(Orthonormal basis)と呼び分ける事にします。
「実は同じもの?」という話がフーリエ変換とか「任意の複雑な波形は(理論上)単純な波の加減算で再現出来る」理論には出てきますが、この時は改めて「周期とは何か(そして無限周期とは?)」みたいな考え方の厳密化を要求されるのです。
0次元多様体(0Dimension Manifold)
観測可能範囲(Observable Range)=実数域(Real)が点となる集合(Set)。
1面多様体(1Sided Manifold)
- 位相学的全体構造(Topological Overall Structure):対角線(Diagonal)=中心点のみが定まった半直線(距離は0~∞の範囲のどれか)の集合
- 実数領域(Real):中心の1点
- 虚数領域(Imaginal):2次元は「半径Rも角度φも未定の円環(ただし半径不明なので円盤の求積に対応)」。3次元は「半径Rも水平角φも垂直角Θも未定の球面(ただし半径不明なので球体求積に対応)」。
すなわちこの段階で既に以下の演算を導入する準備がほとんど整っている。
①まずは鎖鎌で鎖で結び付けられた分銅をブンブン振り回して円や球面を描く状況をイメージして欲しい。

②ずっと動かない「鎌の付け根の支点」を実数域(Real)、「(円や球面を描く)分銅の到達範囲(ただし鎖の長さもが定かでないので実際の範囲は円盤状であったり球体状であったりする)」を虚数域(Imaginal)と捉える。

③さらにこれを対角線集合(Diagonal set)すなわち「中心点から真っすぐ分銅を伸ばした軌跡の集合」と捉える。分銅がどの様な軌跡を描くにせよ(虚数域)、中心からの対角線の観測結果(実数域)は点としかならない訳だが、かかる「数理上における見かけ上の点」は以下の様な数理上の特徴も備えている。
- 角度が絶対的にも相対的にも定かでない以上、各角線の関係を明らかにする事が出来ない。これが統計学でいうところの名義尺度(Nominal Scale)の概念に対応。
- 一方、各対角線上の任意の点は、それぞれの「中心からの距離」が明らかでないにせよ「中心からの順番」だけは観測可能な時がある。これが統計学でいうところの順序尺度(Ordinal Scale)の概念に対応するばかりか「三次元球面座標を二次元表現する場合の符号分け」にも利用される。
そう、人類は悲しい事に「カンブリア爆発期に授かった視覚と視覚情報を処理する脳髄」は例えばこの様に球面を北半球と南半球に分割して把握する事しか出来ないのである。詳しくは次に述べる2面多様体(2Sided Manifold)で扱う。
かかる数学的構造(Mathematical Structure)を、以下では各対角線ごとの座標系を地図(Chart)として捉え地図帳(Atras)として束ね全体構造を俯瞰するのに用いる。
2面多様体(2Sided Manifold)/4面多様体(4Sided Manifold)/8面多様体(8Sided Manifold)
①まずは「表裏しかない(従って厚みを数理的に黙殺し得る)コイン状態の立体」をイメージ。

- オイラーの多面体定理(Eulerian Polyhedron Theore)「V(Vertex=頂点数)-E(Edge=辺数)+F(Face=面数)=2」の平面版を考える。あらゆる多角形(Polyhedron)において頂点数(Number of Vertexs)と辺数(Number of Edges)は一致するので、自明の場合(Trivial-Case)として表裏をカウントしないなら「V-E=0」カウントするなら「V-E+F=2」となる。要するに「一対の多角推を底面で貼り合わせた」状態。
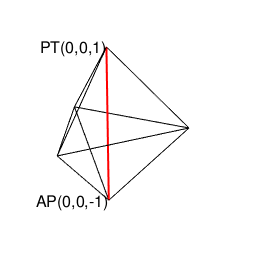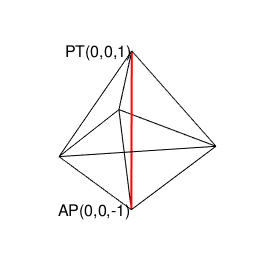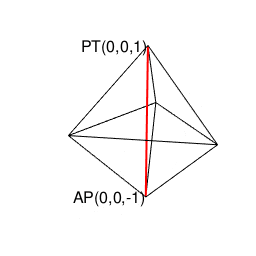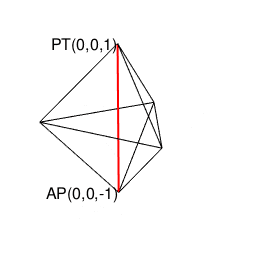
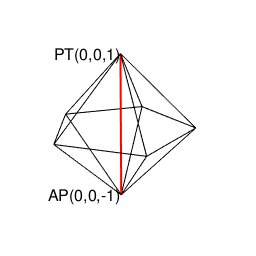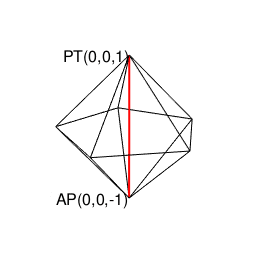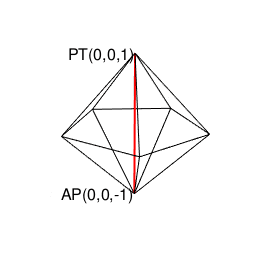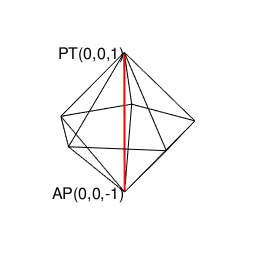
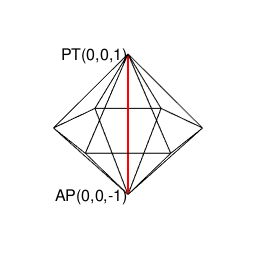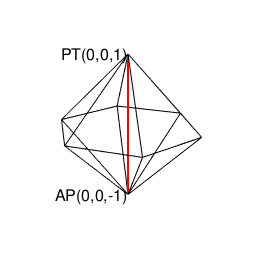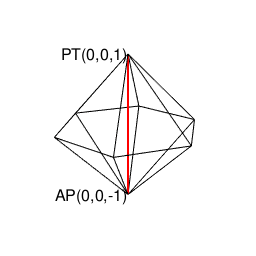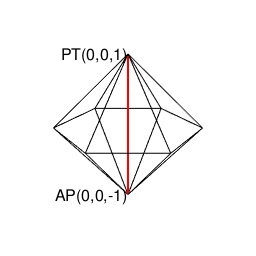
②ところで表(0)は裏(1)、裏(1)は表(0)にしか変遷しない事から、その遷移図を平面的に眺めると、以下の様ないわゆる「二進数格子(Binary Grid)」が現れる。
1-0-1-0-1-0-1-0
0-1-0-1-0-1-0-1
1-0-1-0-1-0-1-0
0-1-0-1-0-1-0-1
1-0-1-0-1-0-1-0

③ただしこの二進数格子、そのまま拡張しても立方体格子座標系(Cube Lattice Coordinate System)でなく、正八面体(Octahedron=立体が対蹠間を結ぶ偶数系立体)と正四面体(Regular Tetrahedron=それぞれ対蹠を起点とする一対で構成される奇数系立体)で立体充填される正三角形格子座標系(Equilateral Triangle Grid Coordinate System)を構成するばかりである。




④いずれにせよ人類は結局、扱いの難しい正三角形格子座標系でなく「(符号問題や偶奇問題を例外として取り除いた上で)辺長1の時に平方対角線は、立方対角線は
」と考える「条件付」立方体格子座標系を採用する道を選んだのだった。ちなみに逆に「対角線長1」から出発すると、これを平方対角線とする辺長は
で立方対角線とする辺長は
(その時現れる立方体の各面の対角線長は
)となる。
ところで何かに気付きませんか?ABC予測を解いた宇宙際タイヒミュラー理論においては「その数理系に導入される素数のかずが増えれ増えるほど展開される数理は複雑化していく」とされますが、本当にそのごくごく最初の部分、すなわち「素数2を巡る数理の全部および素数3を巡る数理の一部」だけを使って構成されてる感じ。

そしてある種の極限値としてこの過程の連続的変遷を扱う三角関数(Trigonometric Function)と実数域(Real)範囲外における回転を扱う虚数域(Imaginal)の概念が登場してくる訳です。
そう、実は人類の大半はプラトン立体(Platonic solid)のうち(それを扱う演算に素数5や素数7が登場する)正十二面体(Regular Dodecahedron)や正二十面体(Regular Icosahedron)について接近を諦める一方…

小学校低学年で習う「掛け算の九九」はそちら側の世界にしっかり踏み込んでたりする訳ですね。エイリアンが跋扈する素数3や素数5や素数7の世界へようこそ?

1次元多様体(1Dimension Manifold)
0次元多様体(実数部)を「点」とイメージした際の「線」のイメージ。
- 位相学的全体構造(Topological Overall Structure):0と「(それ自体は定義も観測も不可能な)+∞と-∞の交点」を対蹠とする円環(二次元)や球面(三次元)。
- 実数領域(Real):0から∞にかけて、あるいは0を中心に-∞から+∞にかけての任意の線状分布(Linear Distribution)、あるいはその2点間を結んだ線分(Line Segment)
- 虚数領域(Imaginal):上掲の位相学的全体構造について(0を中心に据えた)正面図が「(偶数系に分類される)-∞から+∞にかけての線状分布」に、(0を左端か右端に据えた)側面図が「(奇数系に分類される)0から∞にかけての線形分布」にそれぞれ対応。残余部分が虚数領域に分類される。
①もちろん(±)∞そのものは観測も定義も不可能なので「任意の実数の全てについて、それを最大値的に上回る(最小値的に下回る)実数を示す」イプシロンデルタ論法を導入。「観測も定義も不可能な実数域の外側」と向かい合う必要がなくなった。
②記述統計学(Descriptive Statistics)は、母集団の諸元が得られない状況下でも、状況によっては与えられたサンプル集合より暫定的な標本平均(Sample Average)や標本分散(Sample Variance)を得て分布の全体像推定を試みる。さらには二つのサンプル集合の相関係数(Correlation Coefficient)も得られるが、その結果得られる+1~0~-1の数値は三角関数でいうCos(0)~Cos()~Cos(π)の出力結果に対応。
- この様に数理の世界は統計学でいう間隔尺度(Interval Scale)と比例尺度(Ratio Scale)の峻別にそれほど厳格ではない。
- 確率論(Probability Theory)は、この考え方の応用として「それぞれ賞金額も用意される個数も異なるくじ引きのセット」を与えられた場合の「くじびきの結果得られる賞金の期待値(The Expectation Value)」を求める。全体像として特殊な二次元多様体(2Dimension Manifold)を構成する(指数・対数写像によって円グラフと方形グラフの間を往復)。
③この次元以上の多様体には「単位設定(Unit Setting)による定量化(Quantification)」が可能となる。
- 演算
から上掲の正面図を「線長1の線分」無限個に分割した整数加法群(Integer Additive Group,加法単位元=0)が得られる。これにさらに上掲の様な「二進数反転の繰り返し」を重ねようとすると偶奇問題が発生する。10進法などによって実数加法群(Integer Additive Group)を求めた場合には生じなかった問題。
- さらにここで得られた加法群に[-∞→0][0→1][+∞→∞]の写像を施して元群における「乗除算が加減算に置換される」様に調整すると実数乗法群(Real Multiplicative Group,乗法単位元=1,添字0以上が整数の場合、0以下は有理数となる)が得られる。
(スカラー量に対応する)複式簿記やくじ引きセットにおける個数、円/球面座標系における半径、時間推移などの表記については一般に(加法群に立脚する)均等尺を割り当てる。一方、上挙の1次元多様体(事実上の実数列)については、これを垂直軸に設定して直交する水平軸を「(乗法群に立脚する)対数尺の目盛りが乗法単位元1に固定された極座標系(Polar Coordinates System)」と捉えると以降の拡張がやりやすくなる。
円筒座標系(Cylindrical Coordinate System)


ここからそれを含む二次元以上の多様体がどんどん分岐していく訳です。
円錐座標系(Conical Coordinate System)
球面座標系(Spherical Coordinate System)

そしてトーラス座標系(Torus Coordinate System)…
ああ、やっと2018年末に「多分全体像はこんな感じ?」と直感して始めた数学再勉強の成果がそれなりうの形では実った感じ。全ての記録がブログに残ってますが、最初に着手した時点では本当に四元数(Quaternion)や群論(Group Theory)や線形代数(Linear Algebra)はおろか多様体(Manifold)の概念まで組み込まないと全体像が完成しないとは予想だにしていなかったのです。そんな感じで以下続報…