仏教の世界では「(それ自体「色即是空、空即是色」の法則下に置かれている)三昧の世界」に「(それを超越する)桃源郷」を見出してしまうケースを「魔境」と呼んで戒めますが、私の提唱する「数理三昧」の世界に限っては、そういう風に思い上がる余地など一切存在しない様に見て取れます。


例えば群論や線形代数の世界がその幾何学的イメージを置き去りにしてどんどん進んでしまうのに不満を抱いてその部分を補おうと努力してきた訳ですが…まぁ所詮ゴールは同じ訳で、別にそこに新たな発見がある訳でもありません。
まずは数直線概念(Number Line Concept)自体をこう規定します。
整数の除法に由来する商群(Factor Group)によって実数概念(Real Concept)を規定する場合を考える。商群とは任意の整数を例えば10で割った結果得られる(10を法とする)10種類の剰余(0,1,2,3,4,5,6,7,8,9)を元とする集合で、この場合10段階を1周期とする10進法(Decimal System)に対応する。よく知られている様に周期数(周回集合)と段階数(添字集合)を無限に入れ子状態にし続ける事により、その範囲内において任意の実数を表す事ができる。
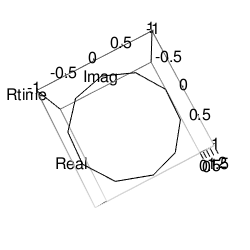
演算上それは(1の冪根の演算結果集合たるガウス巡回群によって得られる)高さと辺数を同じくする多角形螺旋状1次元座標系(Polygonal Spiral One-dimensional Coordinate System)とイメージされる。
その上でこの座標系に周期数(周回集合)や段階数(添字集合)として与えられる加法整数群(Additive Integer Group)を、群論(Group Theory)の原則に従って再定義します。
自然数集合(Natulal Set)+加法単位元(Additive Identity)0

その逆元(Inverse Element)

両者の合算結果としての加法整数群(Additive Integer Group)

ここで「ピッチ問題」が急浮上。この問題を解決する為にΓ関数や偶奇性(Parity)の概念導入が不可避となるのです。
ピッチ1の場合の増減

その水平位置からの観測(周期1のsin(θ)i波の検出)

ピッチ1/2の場合の増減

その水平位置からの観測(周期2のsin(θ)i波の検出)

ところでCos(θ)値の増減に注目するなら、こういう図示も可能です。

ここで気になるのが以下との関連性。
- 一次関数(Linear Function)y=±xやy=±|x|を回転軸とする確率楕円の世界。
- 平面上はcos(θ)のサイクルを適用した楕円の高さの増減によってシミュレーション可能な球面座標上の回転の世界。
そう、どの場合も原則として(立体空間上の円弧の回転操作を側面から観察した)平面空間における楕円の変形過程が「直交する2軸の値の増減の連動」と見て取れるのが特徴で、線形代数(linear Algebra)の世界においては、おそらくここでいう「直交する2軸」が「固有ベクトル(Eigenvector)」、「(連動して変動する)2軸の値」が「固有値(Eigenvalue)」の概念で掌握される展開を迎えると思われるのです(不勉強につき断言までは出来ない)。
要するに現在の私は「あ…ありのまま今起こってる事を話すぜ!「線形代数の固有ベクトルやら固有値の概念がチンプンカンプンなのに、気付いたら実装したプログラム内で勝手にそれらしいのが動いてた。しかもそれが何なのかいまだに全然わからない」。何を言っているのかわからねーと思うが、おれ自身何が起こってるのかさっぱりわかってない。頭がどうにかなりそうだ。催眠術だとか超スピードだとかそんなチャチなもんじゃあ断じてねえ。もっと恐ろしいものの片鱗を味わったぜ…」なるポルナレフ状態…
そして話はズルズルと三次元回転方面に…え、これ中学生の投稿なの?
これまで「(普段遊び場にしている)数理の浜辺」において「波の狭間から仲間にして欲しそうにこちらを見ています。仲間に加えますか?」なる誘い受け自体は幾度となく受けてきましたが「波の狭間から仲間にしたそうにこちらを見ています。仲間にされますか?」なるアプローチを受けたのは初めて。しかもすでに仲間に加えた四元数(Quaternion)から「そいつ、線形独立した軸線しか扱えねぇから」と反対される有様。一体どうしたら良いの?