【数学ロマン】久しぶりの「宇宙的恐怖」との再会。

まぁ、手が付けられないで放っておいた数理に再捕捉されただけな訳ですが…こうやって何度でも以下の言葉に引き戻されるのが数理の世界の醍醐味とも。

フォン・ノイマンは数学はわかることはない、慣れるだけだ、森毅は数学になじみなさいと言っている。

第一の点は、〈数学の概念は、まったく予想外のさまざまな文脈のなかに登場してくる〉ということ。
The first point is that mathematical concepts turn up in entirely unexpected connections.

しかも、予想もしなかった文脈に、予想もしなかったほどぴったりと当てはまって、正確に現象を記述してくれることが多いのだ。
Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections.

第二の点は、予想外の文脈に現れるということと、そしてまた、数学がこれほど役立つ理由を私たちが理解していないことのせいで、〈数学の概念を駆使して、なにか一つの理論が定式化できたとしても、それが唯一の適切な理論なのかどうかがわからない〉ということ。
Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate.

〔この二つの論点をさらに言い直すと〕第一の点は〈数学は自然科学のなかで、ほとんど神秘的なまでに、途方もなく役立っているのに、そのことには何の合理的説明もない〉ということ。
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.

第二の点は〈数学の概念の、まさにこの奇怪な有用性のせいで、物理学の理論の一意性が疑わしく思えてしまう〉ということ。
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories.

こんな世界観、どこまでいっても「完全な理解」など訪れる事はありません。

多くの人は単一の無矛盾的な行動規範を与えれば子どもはすくすくと成長すると考えているけれど、これはまったく愚かな考えであって、これこそ子どもを成熟させないための最も効率的な方法なのである。

成熟というのは簡単に言えば「自分がその問題の解き方を習っていない問題を解く能力」を身に付けることである。

成人の条件というのは「どうふるまってよいかわからないときに、どうふるまうかを知っている」ということである。

例えば、とりあえず私は群論を「クラスをメンバ変数とメンバメソッドの対で考える」オブジェクト志向プログラミングの延長線として把握しています。まずはその表現で語るとどうなるか見ていく事にしましょう。

族(Family)による分類

「そのクラスにおいてメンバメソッドが共有するメンバ変数」に該当する元集合(Element Set)=観測結果集合(Observation Result Set)を族(Family)と規定する。独自表現なので特別にそう呼び分ける事に意義がある場合(すなわち、かかる観測結果集合を共有する演算結果集合が複数存在する事を強調したケース)以外には単に列(Sequence)と呼ぶ。これまで扱ってきたのは以下辺り。

以下に登場する「さしあたって…と規定される」なる表現は、オブジェクト志向プログラミングでいうコンストラクタ（Constructor=オブジェクト生成関数）みたいなイメージ。「族のそれは更新される事がない」という意味合いにおいてある種の定数(集合)として機能する(数学にリテラルの概念が存在しないので、こういう表現にならざるを得ない？)が、もちろん実際のプログラミングの世界は、以下の様な「自然数・整数・実数の規定」の如き数の根本定義を自明の場合(Trival Case)として自動的に言及なく通過してしまう。

①自然数族(Natural Family)/自然数列(Natural Sequence)…観測原点(Observation Origin)0と観測極限(Observation Limit)∞を含まない等間隔に離散する開集合をなす。

$\mathbb{N}_n(n=1→\infty)=(1,2,…,\infty-1)$

さしあたって初項 $α_1=1$ ,公差d=1,一般項 $α_1+(n-1)d$ の無限片側等差数列(One Side Infinity Arithmetic Sequence)の演算結果集合(Operation Result Set)で規定する。
$\mathbb{N}_n(n=1→\infty)=(1+(n-1)d,…)$
周回関数(Rap Function) $1^n(n=-\infty→0→+infty)=(…,1,1,1,…)$ の、とりあえず初項1からの総和、すなわち算術級数列(Arithmetic Series Sequence)もこの族を規定する。
$\mathbb{N}_n(n=1→\infty)=(…,\sum_{k=1}^{n}α_k=\frac{n(2α_1+(n-1)d)}{2},…)$
関数列におけるε-δ論法では連続関数 $\lim_{x \to a}f(x)=f(a)$ の収束がxに依存する場合を各点収束、依存しない場合を一様収束とするが、これは「"とりあえず"が使える=xに依存しない」なので一様収束となるケース? それとも、そもそも収束しないので無関係?

関数列と関数項級

単位元も反元も備えず群を構成しません。どういう事かは以下のアニメーションで直感的に理解可能です。

②整数族(Integer Family)整数列(Integer Sequence)…無限少-∞と無限大+∞を含まない等間隔に離散する開集合をなす。

$\mathbb{Z}_n(n=-\infty→0→+\infty)=(-\infty+1,…,-2,-1,0,1,2,…,+\infty-1)$

さしあたって自然数列 $\mathbb{N}_n$ に単位元0と逆元 $\mathbb{N}_n^{-1}$ を追加する群演算(Group Operation)の演算結果集合で規定する(この操作の結果、観測原点の概念が消失し、観測限界∞が無限小-∞と無限大+∞に分解される点に注意)。その演算集合はZ軸(あるいは時間軸t)における断面曲率の変化を伴わない二次元極座標系、すなわち円筒座標系(Cylindrical Coordinate System)として観測される事になる(虚数(Imaginak)として実軸外部に押し出された円筒半径は理論上どう設定しても良いが、実軸との対応を考えるとそれとの比が1:1と規定するのが最も都合が良い)。
かかる観測結果集合は偶数群2nと奇数集合2n±1の直積、あるいは周期関数(Cyclic Function) $-1^n=±i^{2x}$ と $-1^n±1=±i^{2x}±1$ の直積(ただしn=0→1とし半周単位で分岐切断点を設定した場合)もこの族を規定する(ここで初めて「離散集合をなす整数列の補集合」としての虚数(Imaginal)概念が数理全体の説明として必要不可避となる)。

③実数族(Real Family)実数列(Real Sequence)…無限少-∞と無限大+∞を含まない連続的開集合をなす。

$\mathbb{Z}_n(n=-\infty→0→+\infty)=(-\infty,…,-2,…,-1,…,0,…,1,…,2,…,+\infty)$

さしあたって十進法(Decimal System)すなわち「10を法とする剰余類(0,1,2,3,4,5,6,7,8,9)を添字とする演算結果集合の任意の入れ子状態がなす演算結果集合」で規定する。
「0から2までの正の実数」と2の冪乗算を組み合わせて正の実数に対応させ、これを群演算した演算結果集合もこの族を規定する。
$2^n(n=-\infty→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},…,2^{-1}=\frac{1}{2},…,2^0=\frac{2}{2}=1,…,2^1=2,…,2^2=4,…,2^{+\infty}=\infty)$
2の冪乗算を用いた正の整数の表現例
実数列を(確率の合計を1=100%と計算する)確立密度空間(Probability Density Space)の概念で掌握する統計学(Statistics)の考え方では、間隔尺度(Interval Scale)が「自然数族を十進法導入によって連続化した空間に配置される観測結果集合」、比例尺度(Ratio Scale)が「それにさらに群演算を加えた(すなわち中心を検出して単位元とし、元と逆元を定める操作を経た)連続空間に配置される観測結果集合」に対応し、後者が二群間の相関係数(Correlation Coefficient)や線形回帰性(Linear Regression)などを導出する出発点となる(この操作においても観測原点の概念が消失し、観測限界∞が無限小-∞と無限大+∞に分解される点に注意。データの平均や中央値や最頻値のうちどれかを代表値(Representative Value)に定めた時点から、このプロセスは既に始まっているのである)。

④ネイピア族(Napierian Family)…実数列の指数写像(Exponential Map)と対数写像(Logarithmic Map)を「登り坂の数だけ下り坂がある」観点から併合した独自概念(この演算の無限連続性に触れた説明にまだ出会えてないので仮設定。この辺りから族を単なる、コンピューター言語における定数と看做すのが難しくなってくる)。

この演算結果集合では実数列上における乗除算が対数写像上における加減算に置き換わる。

指数写像(-∞が0、0が1、＋∞が∞に射影される)

$exp(x)(x=-\infty→0→+\infty)=(exp(-\infty)=\frac{1}{exp(\infty)}=0,…,exp(-1)=\frac{1}{exp(1)},…,exp(0)=\frac{exp(1)}{exp(1)}=1,…,exp(1),…,exp(+\infty)=\infty)$

対数写像(直接計算出来ないので、まずは「0から2までの正の対数」とLog(2)の組み合わせから任意の正の対数を求め、さらにその真数部を逆数化した結果を逆元に設定する)。

f:id:ochimusha01:20210504082328p:plain

指数関数や対数関数はしばしばオイラーの公式(Eulerian Formula) $e^{θi}=\cos(θ)+\sin(θ)i$ と紐付けて語られるが、実はこの演算自体はネイピア族に属していない(後述)。その事についてノーベル賞を受賞した物理学者朝永振一郎(1906年～1979年)博士は高校時代から気付いており「中学生には解けない(高校生以上なら解けて不思議でない)問題」と指摘している。この発想がネイピア族と(後述する)ピタゴラス族分離のモチベーションとなった。

つまりネイピア族自体の数理はそれとは異なる形で独自展開する。

例えば生物の神経細胞が持つ性質のモデル化で、ニューラルネットワークにおける活性化関数などで用いられるシグモイド関数(Sigmoid Function) $\frac{1}{1+e^{ax}}=\frac{tanh(\frac{ax}{2})+1}{2}$ などがその代表例の一つ(この辺りを明らかにするのがこれからの課題)。

f:id:ochimusha01:20210504142309p:plain

⑤ピタゴラス族(Pythagorean Family)…さしあたって絶対値(半径)1を与えられたピタゴラスの定理 $x^2+y^2=1$ が描く円弧/球面上の任意の座標集合についての独自表現(以下の概念を網羅する説明にまだ出会えてないので仮設定)。

${半径r^2=x^2+y^2+z^2+…\\特に二次元で半径1の時、y=\sqrt{1-x^2}}$

この集合自体は単位元も反元も備えないので群を構成しない。その辺りの特徴は自然数族と似ている。
(高校数学で習う様な)2項展開(Binomial Expansion) $(a±b)^2$ の範囲では扱い切れず、その証明に「角度が90度(π/2ラジアン)という特別条件」や「複素平面(Complex Plane)における単位円上の操作、すなわち虚数(Imaginal) $i^2=−1$ 概念の導入と共益複素数(Conjugate Complex Number)の相互打ち消し作用」などを必要とする。

全体像はこんな感じとなります。ある意味始まりも終わりもない虚無の世界…

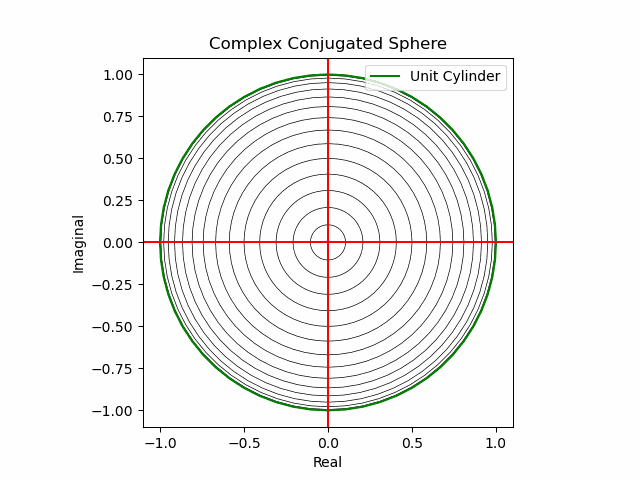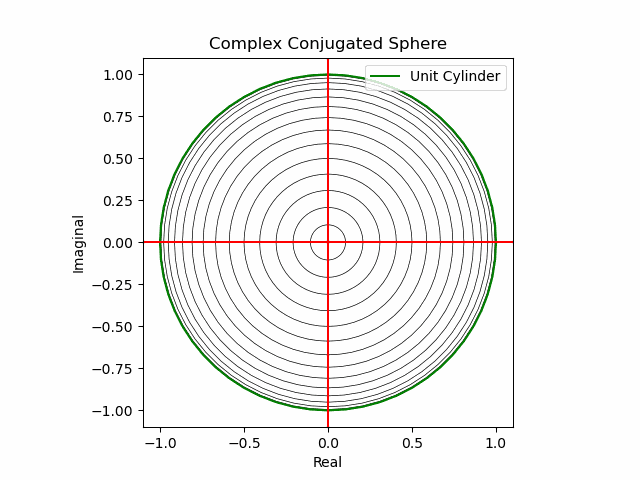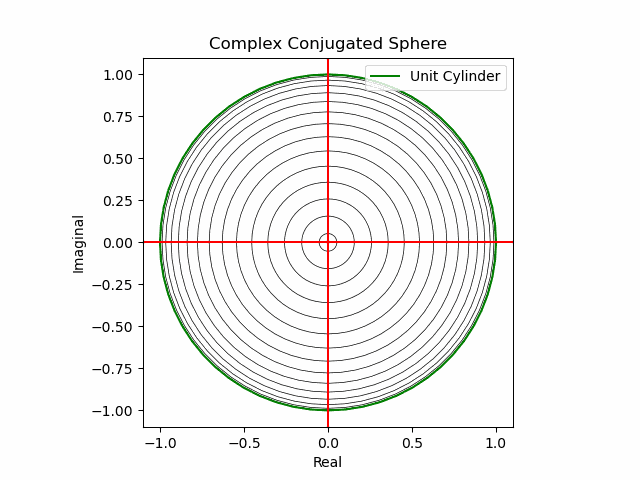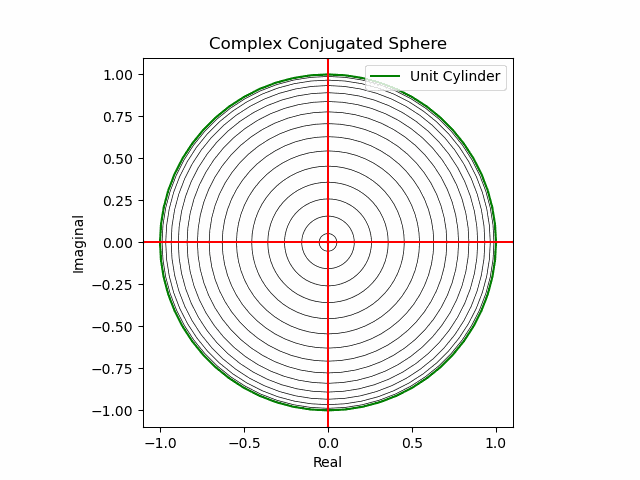
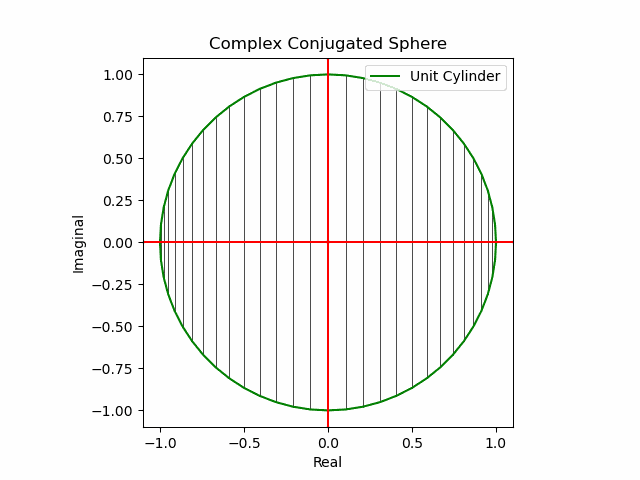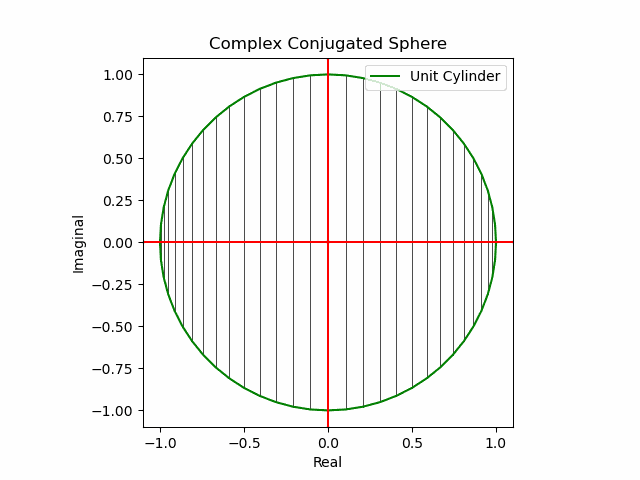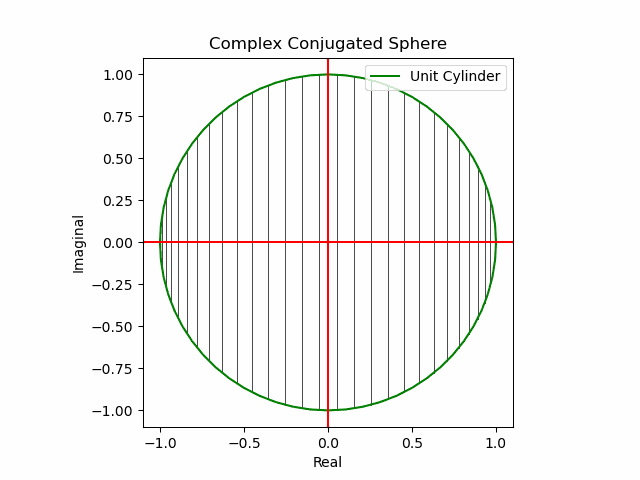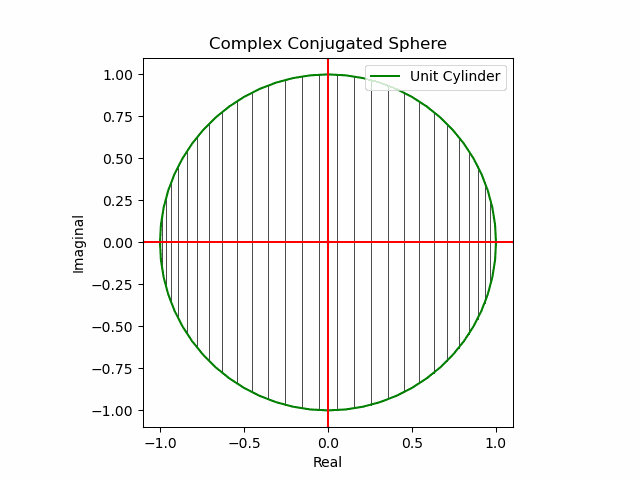
0次元の場合…代数方程式 $x^2+y^2=0$ を解くと $y=±x$ ないしは $x=±y$ となり、かかる一対の線形関数(Linear function)の交点、すなわちxy軸の中心(0,0)、複素平面(Complex Plane)実軸(Real Axis)上の0における点(一切の広がりを備えない半径0の円)としか観測されない。この考え方はN次球へも拡張可能である(任意の次元数上において「点=一切の広がりを備えない半径0の球面」としてしか観測されない)。
1次元の場合…ピタゴラス族と実数列の交点は2点のみ、すなわちxy軸上の(1,0)(-1,0)あるいは複素平面実軸上の-1、1だけとなる。交代級数(Alternating Series)に該当する演算結果集合と重なる。
2次元の場合…代数方程式 $x^2+y^2=1$ を解くと $y=±\sqrt{1-x^2}$ あるいは $x=±\sqrt{1-y^2}$ となり、それぞれ前者はy=0、後者はx=0を分枝切断線(Branch cut line=到達不可能な特異点)とする半円2本を描く。演算結果集合としては単振動(Simple Vibration)[S_n(n=-1 \rightlefthapoons 1)]の「円射影」の結果とも見てとれ(独自表現です)、リー群 $S_0$ に該当する。
3次元の場合…2次元上の展開にさらに範囲-1~1のZ軸を加え、これへの半径0から半径1にかけて断面曲率を円弧に該当する $\sqrt{1-x^2}$ と $\sqrt{1-y^2}$ で与えた結果。演算結果集合としては、これも単振動(Simple Vibration) $SiVi_n(n=-1 \rightleftharpoons 1)$ の「円射影」の一種と見てとれ、リー群 $S_1$ と重なる。

⑤ガウス族(Gauss Family)…「ある母集団から無作為抽出した標本の平均は標本の大きさを大きくすると母平均に近づく」とするベルヌーイの大数弱の法則を拡張して数式化した中心極限定理(CLT=Central Limit Theorem）に対応する観測結果集合。いわゆる正規分布(Normal Distribution)概念の表現としての「ベルカーブ」を指す独自表現。

f:id:ochimusha01:20210504134148p:plain

$f(x)=\frac{1}{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^2}}(-∞<x<+∞)\\確率変数Xの期待値E(X)=平均μ\\確率変数Xの分散V(X)=分散σ^2$

演算結果集合としては放物線関数 $y=-x^2$ の対数写像 $y=e^{-x^2}$ から出発する。実際の統計学で使う式はこの全体を確立密度空間に対応させた複雑な内容となるが、この曲線自体が備える数理的本質そのものは変わらない。
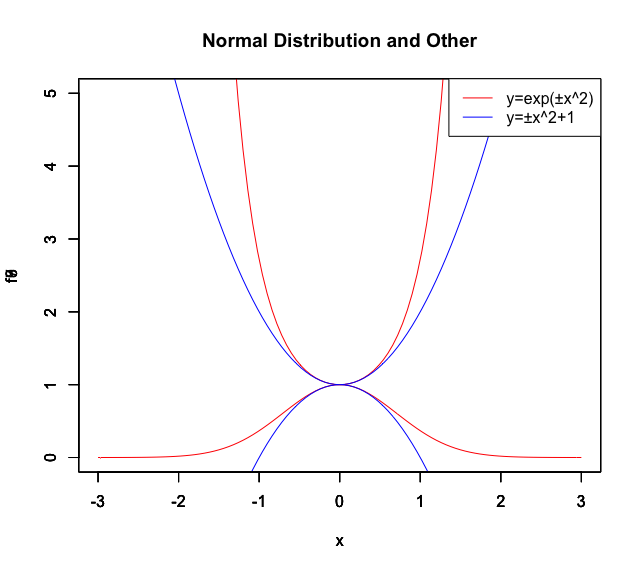
(全体を1=100%と考える確立密度空間における)統計学における相関係数や線形回帰といった数理処理の出発点(観測結果集合を演算結果集合に近づける為に遂行する外れ値除去の技法)でもある。かかる概念は、この演算結果集合を上掲のピタゴラス群に射影するとよりはっきりと見て取れる(通常のピタゴラス群の正面図では中心の反対側の対蹠を観測限界に設定するので裏半分が視野外となるのに対し、この場合は円の辺縁部を観測限界に設定する。その結果「重力レンズ効果によって裏側まで見通せるブラックホールの景観」が現れるが、人間の視覚はこの部分を誤差として切り捨ててしまうので、両者の違いに案外気付かない)。

そもそも媒介変数として離心率εを導入した関数[tex:\frac{1}{1+ε\cos(θ)}](θ=−π→π)において円(楕円)と放物線と双曲線は連続して現れるのです(上掲のピタゴラス族との元の共有範囲は離心率ε=0の場合のみ)。

離心率ε=0の時に半径1の単位円 $y=±\sqrt{1-x^2}$

離心率0<ε<1の時に楕円 $y=\sqrt{b^2(1-\frac{x^2}{a^2})}$

離心率ε=1の時に放物線を横にした $y=\frac{1}{2}±\sqrt{x}$

離心率ε>1の時に双曲線 $y=\sqrt{b^2(\frac{x^2}{a^2}-1)}$

そして離心率εが無限大∞に近くにつれ原点{0,0}へと収束。

ピタゴラス族(Pythagorean Family)を演算結果集合として共有する演算群について。

ところでゲームプログラミングにおける当たり判定(2点間の絶対値を求めて相対距離を計測する)やモンテカルロ法における円の面積や球の体積の算出(ランダムに置かれる点が円/球の内側か外側か判定する)に使われるピタゴラスの定理そのものには、それに含まれる各点の座標を特定する数理が含まれていないのです。

これに対応するのは、また別の演算群(Operation Group)となります。オブジェクト志向プログラミングでいうところの「そのクラスにおいてメンバ変数を共有するメンバメソッド群」に該当。

①ガウスの巡回群(Gauss Cyclic Group)

「正n角形の作図からコンパスと定規を追放した」と言われる、コンピューターグラフィック史上最も重要な演算結果集合の一つ。群論においては、この演算こそが「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスのコンストラクタに指定されています。

1の冪根は全て、複素数平面における単位円周上にある。また概要で述べたことより、1のn乗根の全体は位数nの巡回群である。これは円周群の正規部分群である。

1のn乗根は、複素数平面では、単位円に内接する正n角形の頂点である

代数学的背景はこんな感じ。

数学において公式(Fomura)とは多くの場合恒等式(Identity)を意味するが、その定義は「どの様な値を代入しても両辺が等しくなる」式である。

これに対し「ある特定の値でなければ統合が成立しない式」を方程式(Equatation)と呼び、その値を根(Root)あるいは解(Solution)と言う。

未知数xを含む方程式（Formula）f(x)=0には様々な形式があり、このうち代数的演算（Algebraic operations、加減算、乗除算、冪根）を有限回用いて表せるものを代数方程式（Algebraic Formula）という。

大数学者ガウス(C.F.Gauss, 1777年〜1855年 )は「n次代数方程式はn個の根を複素数の範囲に持つ」事を証明した。これは代数学の基本定理と呼ばれている(ただし四次以上の方程式の解は代数的には求められない)。

「ガウスの巡回群」を図示化した正n角形には興味深い特徴がある。これを元gとして反元 $g^{−1}$ を求めると次数が2n+1(奇数)の場合重ならず、倍の次数2(2n+1)(偶数)で初めて統合されるのである。

おそらく以下の数理も、奇数のこの様な特徴に由来する。
${cos(π)=-1\\cos(\frac{π}{2})=0\\cos(\frac{π}{3})=\frac{1}{2}\\cos(\frac{π}{5})+cos(\frac{3π}{5})=\frac{1}{2}\\cos(\frac{π}{7})+cos(\frac{3π}{7})+cos(\frac{5π}{7})=\frac{1}{2}\\cos(\frac{π}{9})+cos(\frac{3π}{9})+cos(\frac{5π}{9})+cos(\frac{7π}{9})=\frac{1}{2}\\cos(\frac{π}{11})+cos(\frac{3π}{11})+cos(\frac{5π}{11})+cos(\frac{7π}{11})+cos(\frac{9π}{11})=\frac{1}{2}}$
ライプニッツ級数(Leibniz series,1674年,グレゴリー級数がx=1の場合)
$\sum_{n}^{\infty}\frac{-1^n}{2n+1}=\frac{π}{4}$
グレゴリー級数(Gregory series, 1671年)
$\sum_{n}^{\infty}\frac{-1^n}{2n+1}x^{2n+1}=\frac{π}{4}$
ちなみに複素数概念の導入が不可避となるのは三次方程式以上となる。

幾何学的には三角不等式(Triangle Inequality) $‖x+y‖ \leqq ‖x‖+‖y‖$ が成立し面積の概念が生じる「円周上の三点以上の操作」に対応？　そして幸いにも四点までの操作なら「ターレスの定理」により直角の概念が使えるのです。

この様な数学的背景など知らなくても、(代数学的方法では求められないn次方程式を数値的に導出する)以下の計算方法に馴染みがある人なら少なくないはずです。

2πを角数n+1で割った集合θを作る。
それぞれのCos(θ)を求めX軸に置き、Sin(θ)を求めY軸に置く。

そしてこの演算群を導入すると、以下の様な計算も可能となるのです。

一辺の長さがaの正n角形に外接する円の半径r

$r=\frac{a}{2\tan(\frac{π}{n})}$
$a=r(2\tan(\frac{π}{n}))$

一辺の長さがAの正n角形に内接する円の半径R

$R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
$A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$

一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係

$r=Rcos(\frac{π}{n})$
$R=\frac{r}{cos(\frac{π}{n})}$

外接円を単位円（Unit Circle）としたのが上記アニメーション。

外接円の半径Rは単位円の定義に従って1
これに内接する正多辺形の１辺の長さAは $2\tan(\frac{π}{辺数})\cos(\frac{π}{辺数})$
外接円に内接する正多辺形の内接円の半径rは $\cos(\frac{π}{辺数})$

この演算の極限には半径1の単位円の場合における円周長として2πが現れます。半径rの場合に一般化すると算数段階で習う2πrとなりますね。

②極座標系(Polar Coordinates System)表示

ピタゴラス族に含まれる各点の座標を特定する演算結果集合の代表例。

f:id:ochimusha01:20210504154527p:plain

二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換

原点(0,0)からの距離 $r=\sqrt{x^2+y^2}$
$φ=-(\arctan^2(x,y)-\frac{π}{2})$
$x=r×\cos(φ)$
$y=r×\sin(φ)$

三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換

原点(0,0,0)からの距離[tex:r=\sqrt{x^2+y^2+z^2}]
$φ=-(\arctan^2(x,y)-\frac{π}{2})$
$θ=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
$x=r×\sin(θ)\cos(φ)$
$y=r×\sin(θ)\sin(φ)$
$z=r×\cos(θ)$

導出過程で三角関数の加法定理を使っている様です。

$\cos(α+β)=\cos(α)\cos(β)−\sin(α)\sin(β)$
$\cos(α−β)=\cos(α)\cos(β)+\sin(α)sin(β)$
$\sin(α+β)=\sin(α)\cos(β)+\cos(α)\sin(β)$
$\sin(α−β)=\sin(α)\cos(β)−\cos(α)\sin(β)$

垂直角θ(0~πラジアンのπ範囲)を水平角φ(-πラジアン~0~＋πラジアンの2π範囲)の半分に取るのが特徴で、地球儀上で緯度(±90度)の概念が経度(±180度)で表されるのも同じ数理に基づきます。

③円周や表面積や体積を求める公式集合

こちらでまとめて解説しています。

以下はこの演算の中核。球の表面積を求める式 $4πr^2$ や球の体積を求める式 $\frac{4}{3}πr^3$ を導出する三重積分です。

${\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\ =\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix} \frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\ \frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\ \frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ} \end{vmatrix} drdθdφ }$

積分範囲の積み重ね方に注目すると以下となってます。

まずは角度φ=0→2πφ=0→2πの範囲で積分して円周2πrに到達。
さらに角度θ=0→πθ=0→πの範囲で積分を重ね球の表面積 $4πr^2$ に到達。
さらに半径r=0→1r=0→1の範囲で積分を重ね球の体積 $\frac{4}{3}πr^3$ に到達。

極座標系同様、導出過程で垂直角θを水平角φの半分に取ります。同じ演算の別側面と考えるのが正しそうですね。

④オイラーの公式(Eulerien Formula)

これもその演算結果集合が2次元ピタゴラス族=「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスに対応する演算の一つ。角度θによって円周上の位置を指定する形となります。

${e^{iθ}=(1±\frac{πi}{n})^n=\cos(θ)+sin(θ)i\\ 特にθ=πラジアン(180度)の時\\ e^{πi}=-1 }$

この演算からは三角関数と指数・対数関数の関係、微積分の意味などを明らかにする事が出来ます。

$\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
$\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$

f:id:ochimusha01:20210504162020p:plain

f:id:ochimusha01:20210504162153p:plain

$e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
$\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$

式形 $(1±\frac{πi}{n})^n$ はベルヌーイがネイピア数を導出するのに使った式の応用です。

${lim_{n \to \infty}(1±\frac{1}{n})^n=lim_{t \to 0}(t+1)^{1/t}=e^1(2.71828)}$

この式を用いれば「(実数冪のそれとは明らかに異なる)虚数冪の対数写像の振る舞い」を観測出来たりします。

逆を言えば、かかる演算結果集合が二次元ピタゴラス族の場合を説明するのはネイピア数の近似が十分な精度以上の場合に限られる訳です。こうして全体像を俯瞰すると実数冪=ネイピア族と虚数冪=ピタゴラス族をとりあえず切り分けて考える事には相応の意義がありそうなんです。

⑤公比-1の等比数列の演算結果集合

これもその演算結果集合が2次元ピタゴラス族=「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスに対応する演算の一つ。「円射影」される半径上の位置(Cos(θ)とは分布が異なる直径-1~1上の単振動)によって円周上の位置を指定する形となります。

${i^2=-1なので以下となる。\\-1^x=i^2x=(0 \pm 1i)^{2x}\\さらに偶数系の場合は(0 \pm 1i)^{2x}\mp(2n)\\奇数系の場合は(0±1i)^{2x}\mp(2n \pm 1)}$

ただしこの場合もやはり、かかる演算結果集合が二次元ピタゴラス族を説明するのは「周回関数(Rap Function) $1^n$ の冪根「1」が十分1に近く」かつ「周期関数(Cyclyc Function) $-1^n$ の冪根「-1」が十分-1に近い」場合に限られるのです。

公比=1の時…実軸の1の位置に静止。

0<公比<1の時…純粋な1次元展開により０へ向けて収束。

公比>1の時…純粋な1次元展開により無限大に向けて発散。

公比=-1の時…X軸上からは-1と1の間の無限往復に見える。

0>公比>-1の時…振幅の幅が0に向けて狭まっていく。

公比<-1の時…振幅の幅が無限大に向けて広がっていく。

トーラス座標系(Torus Coordinate System)概念の追加。

ところで、ここで2次元ピタゴラス族=「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスなどの直積(Direct Product)を求めると二次元デカルト座標系(2D Cartesian Coordinate System)ではなく二次元トーラス(2D Torus)なる新たな座標系へと進むことになります。

とりあえず最初に現れる大半径(Major Radius)Rと小半径(Minor Radius)rの比率が1:1の場合のトーラスを単位トーラス(Unit Torus)と呼ぶ事にしましょう。

上図の通り、その側面図には2次元ピタゴラス族=「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスが実軸0を中心として2個隣接して現れる。3次元ピタゴラス族=リー群 $S_1$ (実軸0を中心とする半径1の球面)を偶数系(Even System)の起源と置くなら、これが奇数系(Odd System)の起源となる。

この様に二つの半径の組み合わせで表現されるトーラス座標系(Torus Coordinates System)と三次元デカルト座標系(3D Cartesian Coordinate System)の関係は、一般に媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表されます。

f:id:ochimusha01:20210504174439p:plain

$R×\cos(t)+r×\cos(p)\cos(t)$
$R×cos(t)+r×\cos(p)\sin(t)$
$r×\sin(p)$

上掲の円/球面座標系との関係は以下とされています。

大半径R=0,小半径r=1の時、単位球面(Unit Sphere)すなわち三次元ピタゴラス群=リー群 $S_1$ を二重に描く(3次元極座標系や経緯度法で垂直角を水平角の半分に取るのは、この時出る重複部分を除く為)。
逆に大半径R=1,小半径r=0の時、Z=0となってただの単一の単位円(Unit Circle)すなわち2次元ピタゴラス族=「半径1の単位円」を観測結果集合とする円周群=リー群 $S_0$ =1次元トーラスとなる。かかる極限状態に向かう展開は「半径1の単位円に内接する正N角形とそのさらなる内接円の推移(N=∞に近づくほど、どちらの正N角形としての辺長計も円周長2πに限りなく近づいていく)」そのものである。

さらに大半径Rと小半径rの比(Rr比)に注目すると以下の表現となります。

トーラスのRr比が $\frac{\infty}{0}=\infty$ に限りなく近づく時、その全体構造は上掲の「二重球面状態」に向かう。
トーラスの Rr比が $\frac{1}{\infty}=0$ に限りなく近づく時、その全体構造は上掲の「単円弧状態」に向かう。
この考え方では「二重球面状態」や「単円弧状態」自体には到達不可能となるので、その結果得られる観測結果集合や演算結果集合はそれらを含まない開集合となる(この事により「二重球面状態」や「単円弧状態」自体は特異点化する)。

どうやらこの景色はn次球面について(人間が扱える)3次元までの空間概念のみ抽出して操作を加える作業イメージに発展させられそうです。とりあえずその全体像を無限トーラス(Infinity Torus)と呼ぶ事にしましょう。さらに大半径への分枝切断点追加に際して小半径も同様に分割する場合を元、分割数に比例して回転数も上げていく場合を逆元と置けば、分割数1(追加分枝切断点0)を単位元とする乗法群の一種トーラス群(Torus Group)が現れます。

$G_n(n=-\infty→-3→-2→-1→0→1→2→3→+\infty)\\=(\infty,…,4,…,3,…,2,…,1,…,\frac{1}{2},…,\frac{1}{3},…,\frac{1}{4},…,0)$

この過程で上面図に現れる正n角形(1分割状態から始まって辺数無限大、辺長無限小の円弧状態に限りなく近づいていく)は大半径と小半径の比によって一意に定まるので、最終的には $±i^ax$ (a=0→40)関数による表現に統合される形となりそうです。

その一方で、二次元トーラスを平面展開した平坦トーラス(Flat Torus)では1目盛2πの「方眼」が現れますが(分枝点切断前だと)次の升目に移行する概念が存在しません(だからコンピューターRPGのワールドマップの様にグルグル堂々巡りするのみ)。

群論ではこれを「リー群に対して(対数写像によって)接空間リー代数を取る」と表現する様ですが、こちらの系統だと複素関数理論における「多価関数の分枝点切断(Branch Point Cut)」の概念への言及がありません。かかる2次元トーラス上の回転運動の軌跡は、それをアイロンでも掛けたかの様に真っ直ぐ伸ばし、分岐切断して連続させると(デカルト座標系につながる)円筒座標系(Cylindrical Coordinate System)に推移する訳ですが、群論から入るとこの辺りのイメージが掴み難くなってしまうのです。一方、複素関数論の系統では、その場合に自明の場合(Trival Case)として選択肢の一つとして現れる「分枝点を2個設定し、目盛の一升のピッチをπとし、偶奇性(Parity)の概念を追加する」考え方への言及がありません。微積分計算上は「分枝点を1個設定し、目盛の一升のピッチを2πとする」選択の一択だから？

四元数(Quaternion)=三次元トーラスなる概念の追加

ところでリー群は0次元球面 $S_0$ を「半径1の単位円(一次元トーラス=円周群)に対応する円弧(それを構成する実軸上の実数列の全体集合)」、1次元球面 $S_1$ を「半径1の球表面(それを構成する複素数全体の集合)」に対応させる延長線上において、3次元球面 $S_3$ を四元数集合(Quaternion Set)全体に対応させています。

これはおそらく「(原点0を半径0の内周円とし、外周円を半径4πとし、直交する大半径の軌道に沿って進む)二次元トーラス座標上の小半径円」にさらに $\cos(θ)+\sin(θ)i$ の2自由度を加えた場合に相当するのです。

ここで(人間の手に負える)3次元以下のみ抽出して操作を加える無限トーラス上での作業イメージ構築が生きてくる。

とはいえ観察結果集合と演算結果集合が等号で結べるのはオイラーの公式 $e^{θi}$ においてネイピア数eの近似が十分である場合、および周回関数 $1^n$ の冪根が十分1に近く、かつ周期関数 $-1^n±i^{2x}$ のの冪根が十分-1に近い場合に限られる様に、四元数における操作変数(Instrumental Variables)i,j,kも(中心を巡る周回軌道の状態を保ち続ける為に)ある種の相互従属関係を構築し、これが見た目上の交換法則 $x･y=y･x$ の放棄(そちらを選ぶと次の升目に進んでしまう選択肢の排除)につながっていく訳です。

四元数における操作変数i,j,kが以下の関係にあるのは、そういう理由からなんですね。

複素数(どう計算しても隣の升目にはみ出さない)

${i^2=-1\\r(θ)=r±ai\\(a+bi)(c+di)=(ac-bd)+(ad+bc)i}$

このうち(ac-bd)の部分がスカラー積=内積となる。
このうち(ad+bc)の部分がベクトル積=外積となる。

複素数同士の掛算

${α=a+ib,β=c+id\\θ=arg(α),ϕ=arg(β)}$

と置き、これを極座標上での掛け算に置き換えると以下となる。

${α=|α|(\cosθ+i\sinθ)\\β=|β|(\cosϕ+i\sinϕ)\\αβ=|α||β|(\cos(θ+ϕ)+i\sin(θ+ϕ))}$

f:id:ochimusha01:20210505024341p:plain

四元数(隣の升目にはみ出す選択肢の排除を含む)

${i^2=j^2=k^2=ijk=-1\\r(θ,φ)=r±ai±bj±ck\\(ai+bj+ck)(di+ej+fk)=−1*(ad+be+cf)+(bf−ce)i+(cd−af)j+(ae−bd)k}$

このうち(ad+be+cf)の部分がスカラー積=内積となる。
このうち(bf−ce)i+(cd−af)j+(ae−bd)kの部分がベクトル積=外積となる。

どうやらこの辺りの話、テイラー展開を特異点を超えて遂行可能としたローラン展開が「複素数が描く閉曲線の面積の総和は0となる」数理に立脚している事と何やら関係がありそうな…

そんな感じで以下続報。2019年末に「数理再勉強」を宣言した時点では、こういう「全然理解自体は進まないのに、慣れた事で少しずつ前には進める様になっていく(そして今でもコンピューターの援用なしにはこうした概念が振り回せない!!)」感覚が想像すら出来ませんでした。それが分かっただけでも十分な収穫と言えそう？