「自分には数理が足りてない」と自覚して数学再勉強を始めて3年目…途中から是非手掛けたいと思う様になったアニメーションを仕上げる事に成功しました。



群論における空環概念は空和概念と空積概念で構成されています。
空積概念(Empty/Nullary Product Concept)
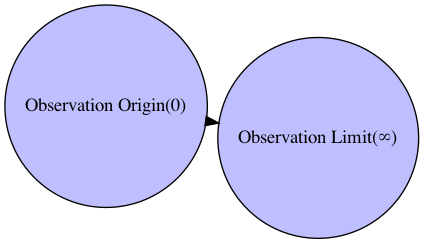
- 観測限界(Observation Limit)∞を点と置いた場合、観測原点(Observation Origin)0との距離x(範囲0~∞)は、何倍にしても何分の1にしても値は変わらない。
- ただし例外的に
となり、これが乗法単位元(Multiplicative Identity)概念の出発点となる。
空和概念(Empty/Nullary Sum Concept)
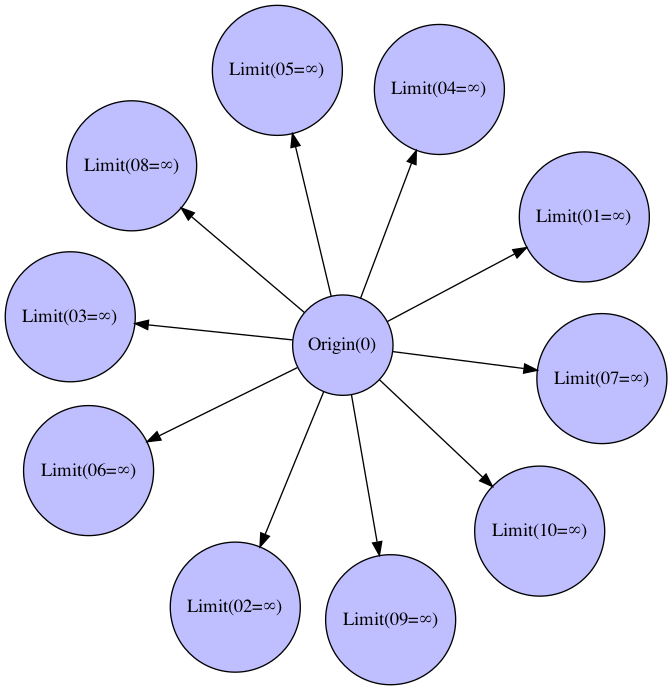
- 観測限界∞を観測原点0との距離x(範囲0~∞)を半径とする円弧/球面と置いた場合、それをどんなに足し合わせても値は変わらない。
- ただし例外的にx−x=0となり、これが加法単位元(Additive Identity Identity)の概念の出発点になる。
そして両者を指数・対数写像によって統合する様子を描いたのが上掲アニメーションなんですね。詳しい話は以下続報…