まさにタイムリーにこの話だ?
科学への一般人の理解が、最近の「スゴイ」研究者を宣伝する風潮により、「孤独な天才科学者」が突然の大発見で科学を発展させるとの「神話」が世間に流布。然し現実は、科学者達は互いに影響を与え、協働し、一段づつ繋がった研究で科学を発展させている。少数科学者への過剰な「選択と集中」は有害。 https://t.co/XyKO72j4bb
— Norio Nakatsuji (@norionakatsuji) November 8, 2019
ノーベル賞が”個人”に与えられるという伝統も影響していると思います。知におけるパラダイム転換と集団知の問題は一筋縄ではいかないですね。
— トマトの気持ち (@tomatosukisuki1) November 8, 2019
だから、ある分野を代表して自分は受賞したという自覚と、大きな名誉を与えられたので、自分周辺だけではなく、広く科学や学問に対する社会的支援を促すような言動が、ノーベル賞受賞者には求められている。
— Norio Nakatsuji (@norionakatsuji) November 9, 2019
極論を言うと『研究成果=知』はすべて集合知であって純粋な個人に属する知的財産などはありえないと言えると思います。今の日本では集合知の構築に職業として参加する人々(いわゆる学者さん)を養う(失礼な言葉で申し訳ないですが)システムが崩壊しようとしているのではないかと危惧しています。
— トマトの気持ち (@tomatosukisuki1) November 9, 2019
どうしてオイラーの公式(Euler's formula)e^θi=cos(θ)+sin(θ)i(理論値)=(1±θi/N)^N(大数弱の法則の証明)を巡る知識は莫大なコンセンサスを蓄えているのに…
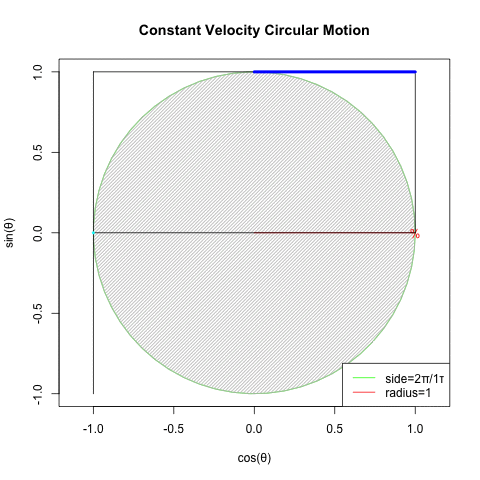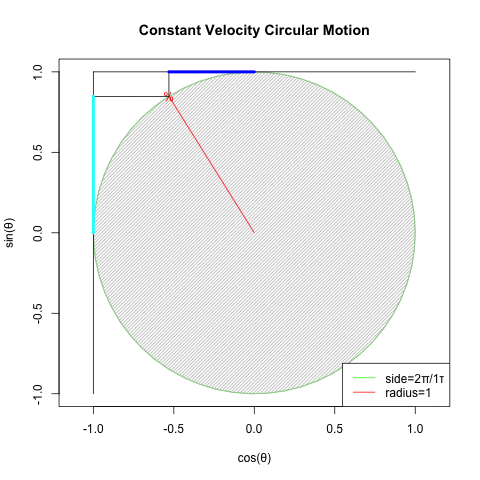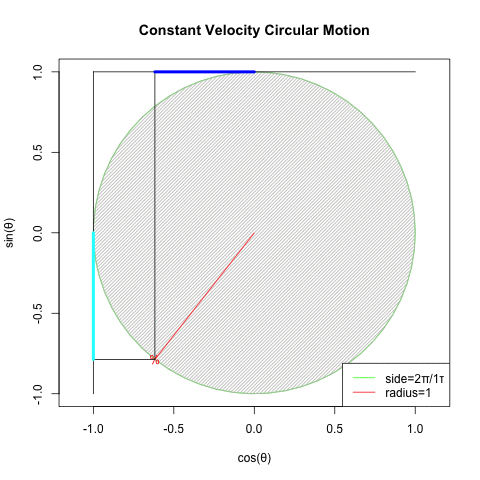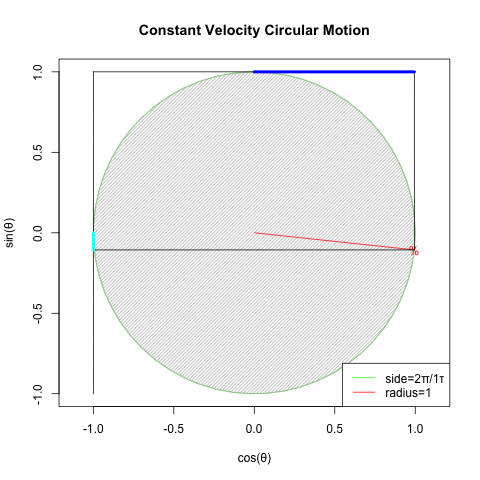
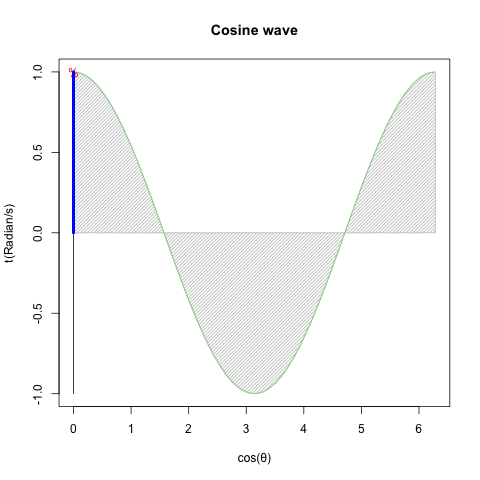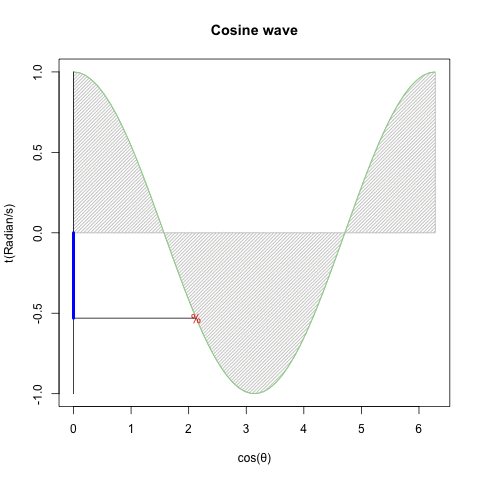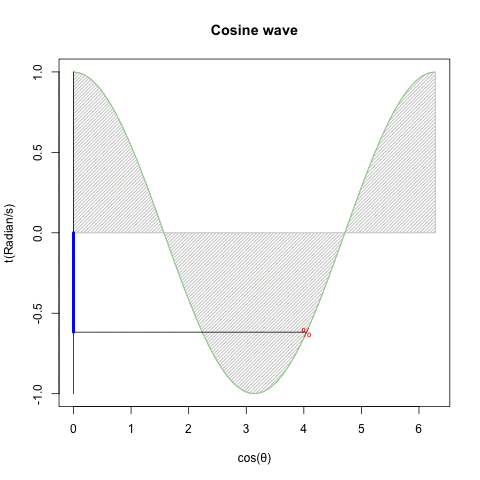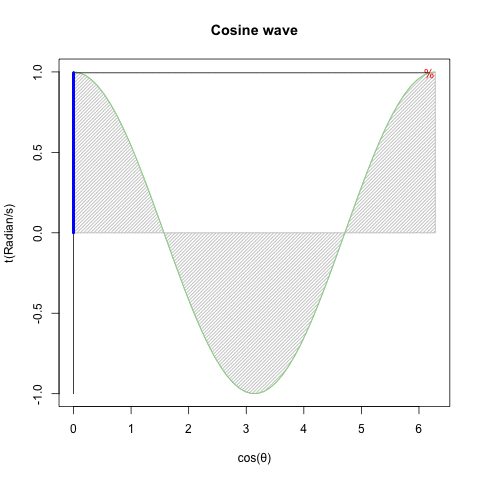

とはいえ、既にネイピア数の算出式たる(1±1/N)^N(大数弱の法則の証明)に比べて既に(1±θi/N)^Nの形に関する言及は極端に減少する訳ですが…
*正直今でも思ってるくらい。「(1±1/N)^Nの式にθiをぶち込む事を思いついた人間は、ナマコを最初に食べた人間と尻の穴に突っ込んだ人間と同じくらいとんでもない」と。
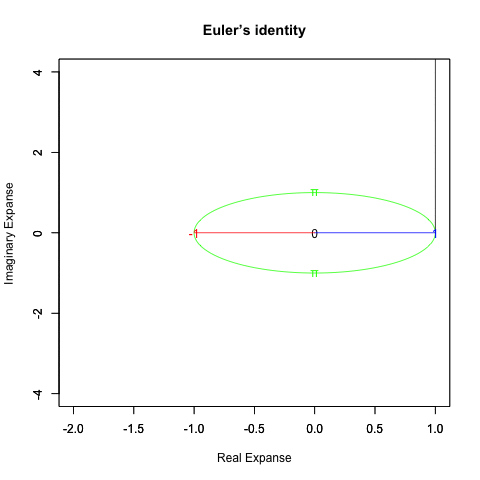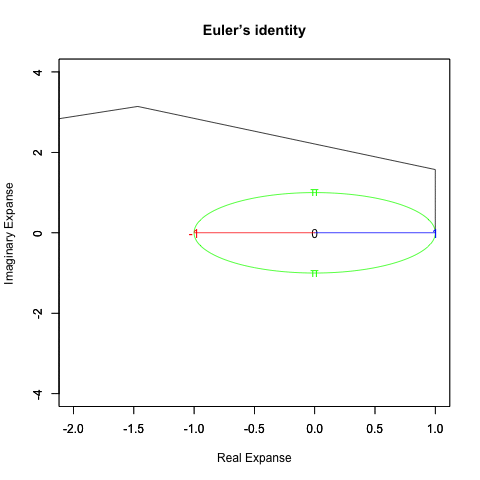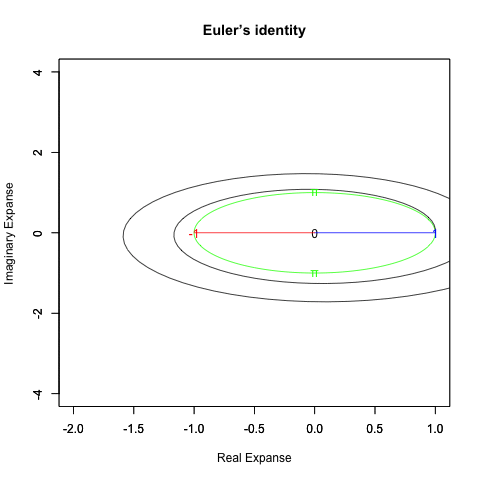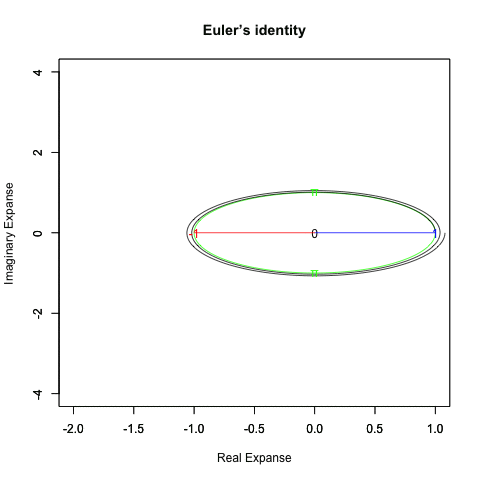
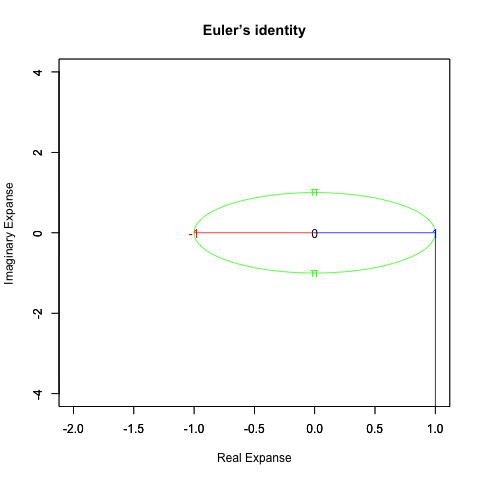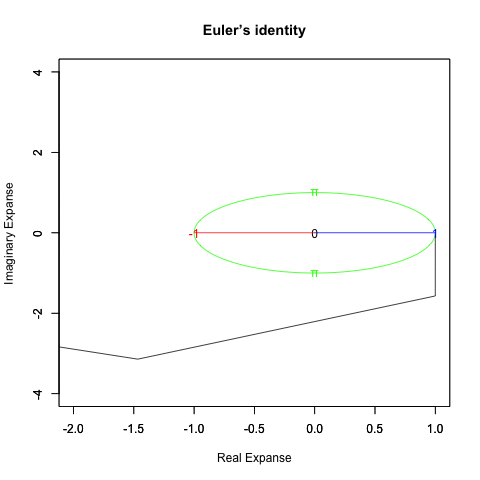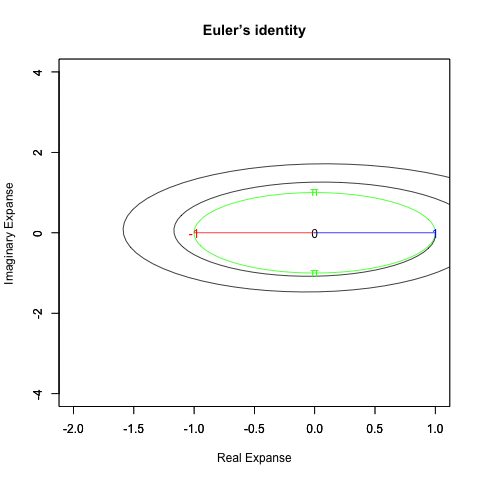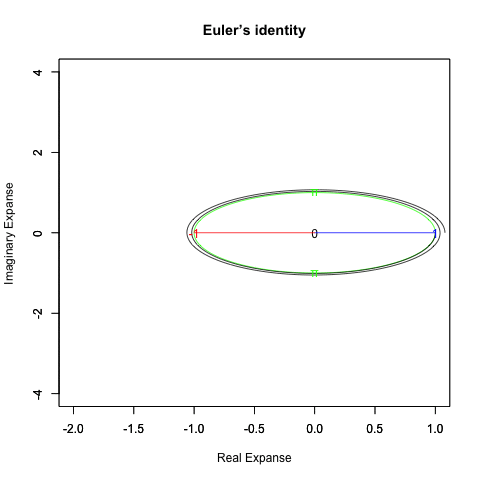
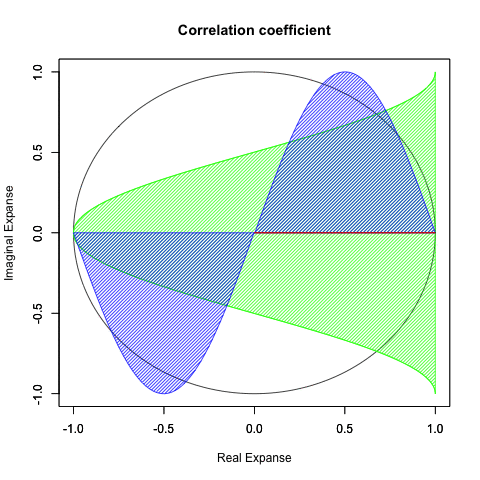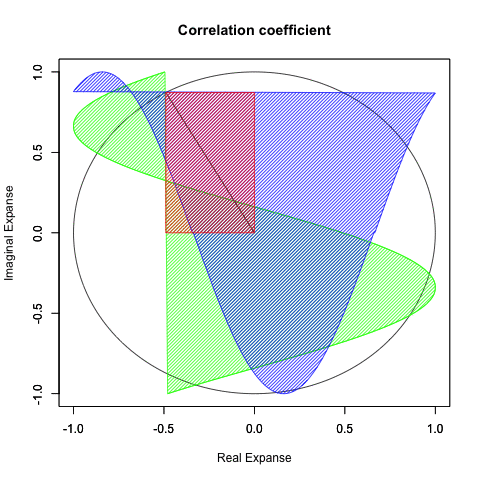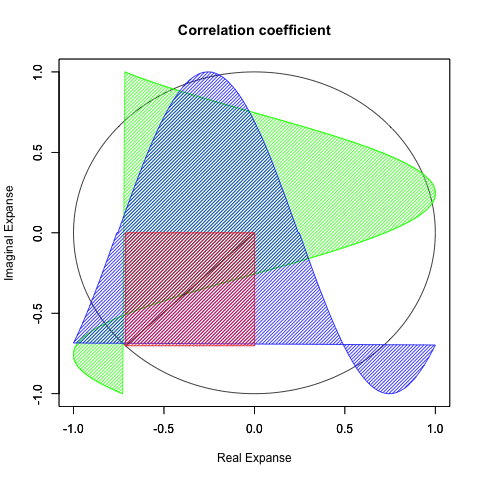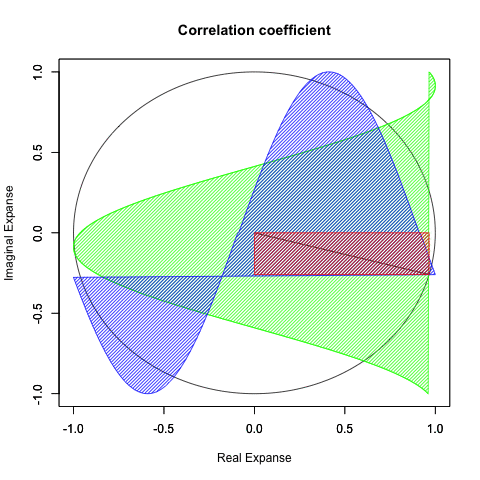
さらに一般形ともいうべき正多辺形方程式(Regular Polisides equattion)」Cos(θ)+Cos(θ-π/NoC)iについての知識となると(どうやら「確率密度楕円」なる認識と関わってる事が次第に明らかになりつつあるとはいえ)徹底して未整備。


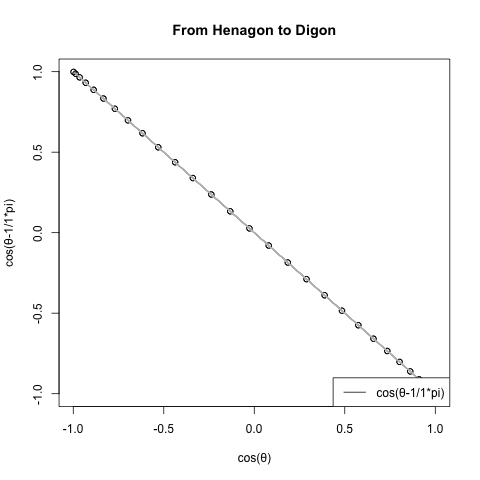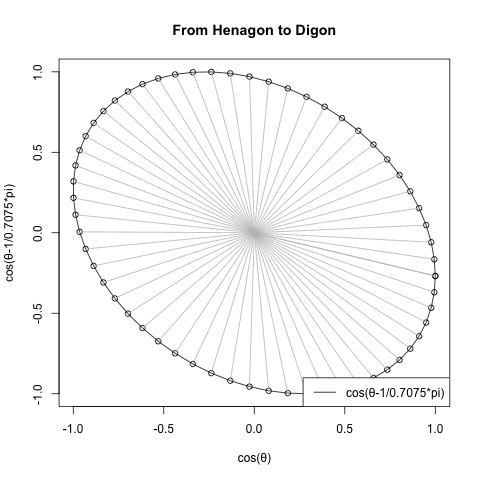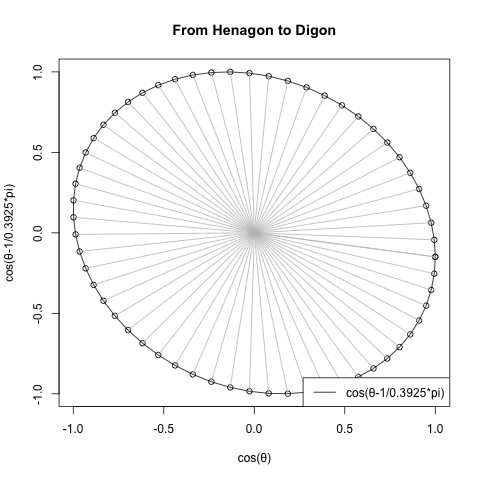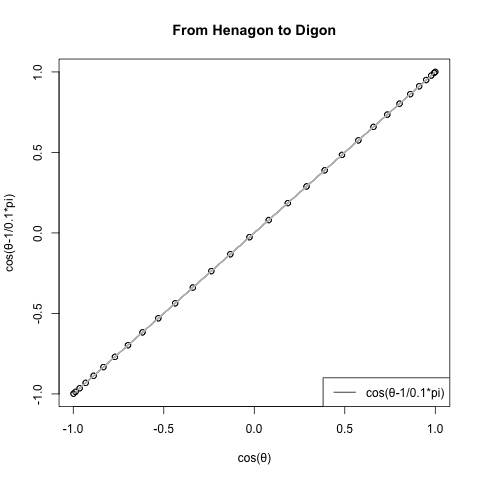

*原因は簡単で「3角形以下の角数の多角形は存在しない」なるユークリッド幾何学的常識が認識の邪魔をするのである。皮肉にもこの常識を突破するにはWikipediaの以下の記述が役立つ。
これはもう「関わってきた研究者の数」としか言い様がないんですね。もちろんこれらの科学知識の実用性や既存知識との相性とも深く関わって来るのでしょうけど。
人工知能が「地球は太陽の周りを回っている」という事実に気づく。人類が何世紀もかけた問題をいとも容易く…
— 大丸拓郎|Takuro Daimaru (@takurodaimaru) November 9, 2019
人間の脳の構造に基づく新型のニューラルネットワークを使った研究。今後は同じ技術で新しい物理法則を発見することを目指すそう。
ついにここまできたか…https://t.co/OVufiAyrgC
従来のニューラルネットワークは例えば猫の画像を与え続けると学習の結果「足が4本あって耳が尖ってる」のような解を出してくるんだけど、
— 大丸拓郎|Takuro Daimaru (@takurodaimaru) November 9, 2019
新型のNNは2部分に別れていて、1つ目が抽出した特徴を2つ目が「足が4本あって耳が尖ってるのは猫!」みたいにこれまでの経験を使って答えを出してくるらしい。
例えばこのNNに物理現象が含まれてるかもしれないけど人間が見落としてしまうくらい巨大なデータセットを与えると、新たな物理法則がはじき出されるかもしれないという話。
— 大丸拓郎|Takuro Daimaru (@takurodaimaru) November 9, 2019
それでも最終的な答えは数式で出てくるので、それを解釈できるくらいに人間が賢い必要はあると。
概念的なのものでまだ実装はされていない感じですか?
— 霧隠@2日目西Lー16b (@det_kirigakure) November 10, 2019
— ༻ L♡VED♡LL ༺ (@ai_ningyo) November 10, 2019
考察して出した結果を、人間が得た経験則を使って解析するのか…経験が積み上がった分だけ正確性が持ち上がる事になりますね。人類知性が数千年で追い越されるなあ。こわいこわい。
— 珍小鳥@短歌を詠み小説を書くアライさんbot (@chinkotori_fake) November 10, 2019
本当に「追い越せる」のかなぁ。例えば最近私が追っかけてる「45度の秘密」…


集まってくるエビデンス全てが「システム全体にどうやって2を底とする指数・対数比が組み込まれてるか」がヒントだと示してる訳ですが、むしろそこから先が長い…もしかしたら(当時発見されたばかりだった)テイラー/マクローリン級数(Taylor/Maclauri series)を用いてe^θi=cos(θ)+sin(θ)iの式を証明したオイラー自身がガウス平面(Zahlenebene)までは到達出来なかった様に、たった一人の自力で解決するのは不可能かもしれない…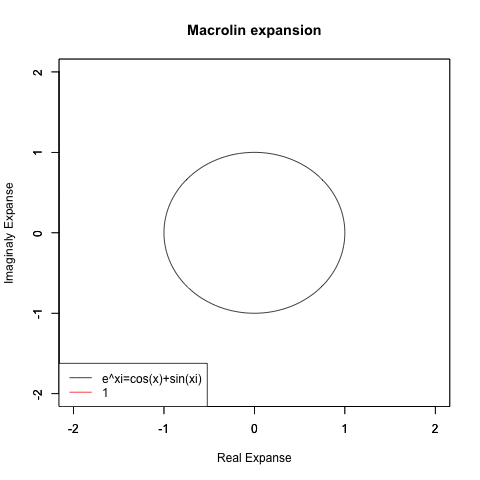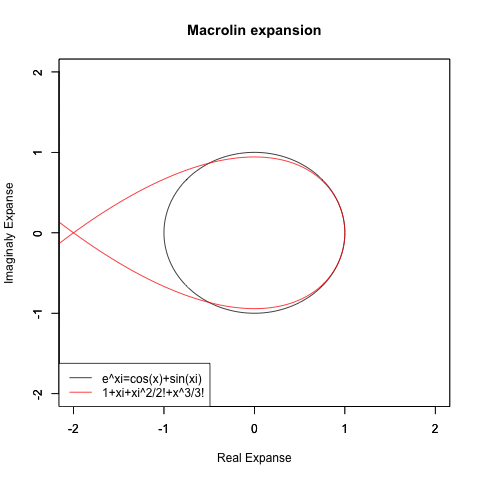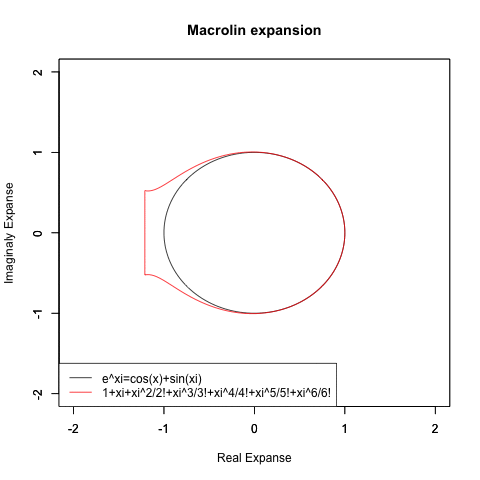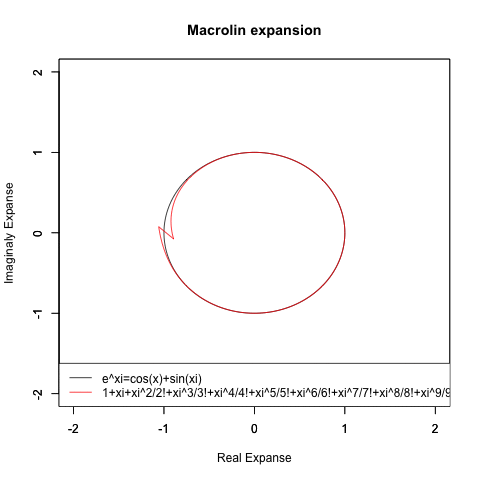
最近、山本義隆「少数と対数の発見」を読んで「整数の離散尺度から実数の連続量尺度への飛躍」がどうやって達成されてきたか知ったばかり。
上記の一連の数学者たちの生没年を眺めると、ほとんどが同時代人(16世紀中頃―17世紀前半)である。小数や対数が発見され成立する時代は、先の三部作で明らかにされた16―17世紀における近代科学誕生の前史の時代とほぼ重なっていることがわかる。そのことは、近代科学誕生の前史を基礎づけ構築してきた人物たちが、それらと並走しながら、新たな数の概念を創り出したことを物語っている。
彼らの創り出した数学は、数学のための数学ではなく、多様な現場で要求される実用性を重んじる応用数学であった。この実用性を重んじる応用数学を創造する営みは、考察の対象とされるすべての数学者たちに共通して見られる現象である。
そして、さらにその前史としてアフリカ十字軍の「不帰の岬として恐れられていた西サハラのボジャドール岬のポルトガル騎士修道会の突破(1434年)」なる地球平面説に致命傷を与えた展開があったという次第。
自分がこういう問題に巻き込まれて初めて上掲の話題が心に染みて来るという…
「神は人間に自力解決不可能な問題を掲示なさらない」なる米国実用主義者(pragmatist)の魂の叫びの本質が、やはり宗教的な内面性を備えていた事を思い知るという…